set.hh File Reference
(Revision: 3477)
#include "gecode/limits.hh"
#include "gecode/kernel.hh"
#include "gecode/int.hh"
#include "gecode/set/exception.icc"
#include "gecode/set/var.icc"
#include "gecode/set/view.icc"
#include "gecode/set/propagator.icc"
#include "gecode/set/array.icc"
Go to the source code of this file.
Namespaces | |
| namespace | Gecode |
| namespace | Gecode::Set |
Defines | |
| #define | GECODE_SET_EXPORT |
Enumerations | |
| enum | Gecode::SetRelType { Gecode::SRT_EQ, Gecode::SRT_NQ, Gecode::SRT_SUB, Gecode::SRT_SUP, Gecode::SRT_DISJ, Gecode::SRT_CMPL } |
| Common relation types for sets. More... | |
| enum | Gecode::SetOpType { Gecode::SOT_UNION, Gecode::SOT_DUNION, Gecode::SOT_INTER, Gecode::SOT_MINUS } |
| Common operations for sets. More... | |
| enum | Gecode::SetBvarSel { Gecode::SETBVAR_NONE, Gecode::SETBVAR_MIN_CARD, Gecode::SETBVAR_MAX_CARD, Gecode::SETBVAR_MIN_UNKNOWN_ELEM, Gecode::SETBVAR_MAX_UNKNOWN_ELEM } |
| Which variable to select for branching. More... | |
| enum | Gecode::SetBvalSel { Gecode::SETBVAL_MIN, Gecode::SETBVAL_MAX } |
| Which values to select first for branching. More... | |
Functions | |
| void | Gecode::dom (Space *home, SetVar x, SetRelType r, int i) |
Propagates 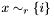 . . | |
| void | Gecode::dom (Space *home, SetVar x, SetRelType r, int i, int j) |
Propagates 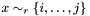 . . | |
| void | Gecode::dom (Space *home, SetVar x, SetRelType r, const IntSet &s) |
Propagates 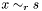 . . | |
| void | Gecode::dom (Space *home, SetVar x, SetRelType r, int i, BoolVar b) |
Post propagator for 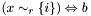 . . | |
| void | Gecode::dom (Space *home, SetVar x, SetRelType r, int i, int j, BoolVar b) |
Post propagator for 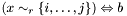 . . | |
| void | Gecode::dom (Space *home, SetVar x, SetRelType r, const IntSet &s, BoolVar b) |
Post propagator for 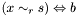 . . | |
| void | Gecode::cardinality (Space *home, SetVar x, unsigned int i, unsigned int j) |
Propagates 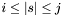 . . | |
| void | Gecode::rel (Space *home, SetVar x, SetRelType r, SetVar y) |
Post propagator for 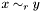 . . | |
| void | Gecode::rel (Space *home, SetVar x, SetRelType r, SetVar y, BoolVar b) |
Post propagator for 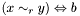 . . | |
| void | Gecode::rel (Space *home, SetVar s, SetRelType r, IntVar x) |
Post propagator for 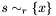 . . | |
| void | Gecode::rel (Space *home, IntVar x, SetRelType r, SetVar s) |
Post propagator for 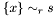 . . | |
| void | Gecode::rel (Space *home, SetVar s, SetRelType r, IntVar x, BoolVar b) |
Post propagator for 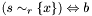 . . | |
| void | Gecode::rel (Space *home, IntVar x, SetRelType r, SetVar s, BoolVar b) |
Post propagator for 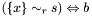 . . | |
| void | Gecode::rel (Space *home, SetVar s, IntRelType r, IntVar x) |
Post propagator for 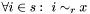 . . | |
| void | Gecode::rel (Space *home, IntVar x, IntRelType r, SetVar s) |
Post propagator for 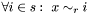 . . | |
| void | Gecode::rel (Space *home, SetVar x, SetOpType op, SetVar y, SetRelType r, SetVar z) |
Post propagator for  . . | |
| void | Gecode::rel (Space *home, SetOpType op, const SetVarArgs &x, SetVar y) |
Post propagator for 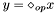 . . | |
| void | Gecode::rel (Space *home, SetOpType op, const IntVarArgs &x, SetVar y) |
Post propagator for 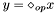 . . | |
| void | Gecode::rel (Space *home, const IntSet &x, SetOpType op, SetVar y, SetRelType r, SetVar z) |
Post propagator for  . . | |
| void | Gecode::rel (Space *home, SetVar x, SetOpType op, const IntSet &y, SetRelType r, SetVar z) |
Post propagator for  . . | |
| void | Gecode::rel (Space *home, SetVar x, SetOpType op, SetVar y, SetRelType r, const IntSet &z) |
Post propagator for  . . | |
| void | Gecode::rel (Space *home, const IntSet &x, SetOpType op, const IntSet &y, SetRelType r, SetVar z) |
Post propagator for  . . | |
| void | Gecode::rel (Space *home, const IntSet &x, SetOpType op, SetVar y, SetRelType r, const IntSet &z) |
Post propagator for  . . | |
| void | Gecode::rel (Space *home, SetVar x, SetOpType op, const IntSet &y, SetRelType r, const IntSet &z) |
Post propagator for  . . | |
| void | Gecode::convex (Space *home, SetVar x) |
| Post propagator that propagates that x is convex. | |
| void | Gecode::convexHull (Space *home, SetVar x, SetVar y) |
| Post propagator that propagates that y is the convex hull of x. | |
| void | Gecode::sequence (Space *home, const SetVarArgs &x) |
Post propagator for 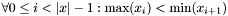 . . | |
| void | Gecode::sequentialUnion (Space *home, const SetVarArgs &y, SetVar x) |
Post propagator for 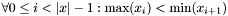 and and 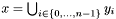 . . | |
| void | Gecode::atmostOne (Space *home, const SetVarArgs &x, unsigned int c) |
Post propagator for 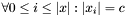 and and 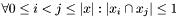 . . | |
| void | Gecode::distinct (Space *home, const SetVarArgs &x, unsigned int c) |
Post propagator for 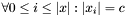 and and 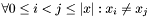 . . | |
| void | Gecode::min (Space *home, SetVar s, IntVar x) |
| Post propagator that propagates that x is the minimal element of s. | |
| void | Gecode::max (Space *home, SetVar s, IntVar x) |
| Post propagator that propagates that x is the maximal element of s. | |
| void | Gecode::match (Space *home, SetVar s, const IntVarArgs &x) |
Post propagator that propagates that s contains the 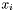 , which are sorted in non-descending order. , which are sorted in non-descending order. | |
| void | Gecode::channel (Space *home, const IntVarArgs &x, const SetVarArgs &y) |
Post propagator for 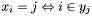 . . | |
| void | Gecode::cardinality (Space *home, SetVar s, IntVar x) |
Post propagator for 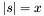 . . | |
| void | Gecode::weights (Space *home, const IntArgs &elements, const IntArgs &weights, SetVar x, IntVar y) |
Post propagator for 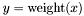 . . | |
| void | Gecode::selectUnion (Space *home, const SetVarArgs &x, SetVar y, SetVar z) |
Post propagator for ![$ z=\bigcup\langle x_0,\dots,x_{n-1}\rangle[y] $](form_342.png) If y is the empty set, z will also be constrained to be empty (as an empty union is empty). If y is the empty set, z will also be constrained to be empty (as an empty union is empty). | |
| void | Gecode::selectInter (Space *home, const SetVarArgs &x, SetVar y, SetVar z) |
| void | Gecode::selectInterIn (Space *home, const SetVarArgs &x, SetVar y, SetVar z, const IntSet &universe) |
| void | Gecode::selectDisjoint (Space *home, const SetVarArgs &x, SetVar y) |
Post propagator for ![$ \parallel\langle x_0,\dots,x_{n-1}\rangle[y] $](form_306.png) . . | |
| void | Gecode::selectSet (Space *home, const SetVarArgs &x, IntVar y, SetVar z) |
Post propagator for ![$ z=\langle x_0,\dots,x_{n-1}\rangle[y] $](form_344.png) . . | |
| void | Gecode::branch (Space *home, const SetVarArgs &x, SetBvarSel vars, SetBvalSel vals) |
| Branch over all x with variable selection vars and value selection vals. | |
Define Documentation
|
|
|
