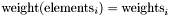Connection constraints to finite domain variables
[Using finite integer sets]
Collaboration diagram for Connection constraints to finite domain variables:

|
Functions | |
| void | Gecode::min (Space *home, SetVar s, IntVar x) |
| Post propagator that propagates that x is the minimal element of s. | |
| void | Gecode::max (Space *home, SetVar s, IntVar x) |
| Post propagator that propagates that x is the maximal element of s. | |
| void | Gecode::match (Space *home, SetVar s, const IntVarArgs &x) |
Post propagator that propagates that s contains the 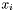 , which are sorted in non-descending order. , which are sorted in non-descending order. | |
| void | Gecode::channel (Space *home, const IntVarArgs &x, const SetVarArgs &y) |
Post propagator for 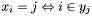 . . | |
| void | Gecode::cardinality (Space *home, SetVar s, IntVar x) |
Post propagator for 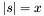 . . | |
| void | Gecode::weights (Space *home, const IntArgs &elements, const IntArgs &weights, SetVar x, IntVar y) |
Post propagator for 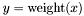 . . | |
Function Documentation
|
||||||||||||||||
|
Post propagator that propagates that x is the minimal element of s.
|
|
||||||||||||||||
|
Post propagator that propagates that x is the maximal element of s.
|
|
||||||||||||||||
|
Post propagator that propagates that s contains the
|
|
||||||||||||||||
|
Post propagator for
|
|
||||||||||||||||
|
Post propagator for
Definition at line 42 of file cardinality.cc. |
|
||||||||||||||||||||||||
|
Post propagator for
The weights are given as pairs of elements and their weight: The upper bound of x is constrained to contain only elements from elements. The weight of a set is the sum of the weights of its elements. |