Gecode::Int::Sorted Namespace Reference
Detailed Description
Sorted propagators
Classes | |
| class | Rank |
| Storage class for mininmum and maximum of a variable. More... | |
| class | SccComponent |
| Representation of a strongly connected component. More... | |
| class | OfflineMinItem |
| Item used to construct the OfflineMin sequence. More... | |
| class | OfflineMin |
| Offline-Min datastructure Used to compute the perfect matching between the unsorted views x and the sorted views y. More... | |
| class | TupleMaxInc |
| Index comparison for ViewArray<Tuple>. More... | |
| class | TupleMaxIncExt |
| Extended Index comparison for ViewArray<Tuple>. More... | |
| class | TupleMinInc |
| View comparison on ViewTuples. More... | |
| class | ViewPair |
| Extended View comparison on ViewTuples. More... | |
| class | TupleMinIncExt |
| class | Sorted |
| Bounds consistent sortedness propagator. More... | |
Functions | |
| template<class View> | |
| bool | glover (ViewArray< View > &x, ViewArray< View > &y, int tau[], int phi[], OfflineMinItem sequence[], int vertices[]) |
| Glover's maximum matching in a bipartite graph. | |
| template<class View> | |
| bool | revglover (ViewArray< View > &x, ViewArray< View > &y, int tau[], int phiprime[], OfflineMinItem sequence[], int vertices[]) |
| Symmetric glover function for the upper domain bounds. | |
| template<class View> | |
| void | computesccs (ViewArray< View > &x, ViewArray< View > &y, int phi[], SccComponent sinfo[], int scclist[]) |
| Compute the sccs of the oriented intersection-graph. | |
| template<class View, bool Perm> | |
| bool | narrow_domx (Space *home, ViewArray< View > &x, ViewArray< View > &y, ViewArray< View > &z, int tau[], int[], int scclist[], SccComponent sinfo[], bool &nofix) |
| Narrowing the domains of the x variables. | |
| template<class View> | |
| bool | narrow_domy (Space *home, ViewArray< View > &x, ViewArray< View > &y, int phi[], int phiprime[], bool &nofix) |
| Narrowing the domains of the y views. | |
| template<class View, bool Perm> | |
| void | sort_sigma (ViewArray< View > &x, ViewArray< View > &z) |
Build 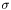 . . | |
| template<class View, bool Perm> | |
| void | sort_tau (ViewArray< View > &x, ViewArray< View > &z, int tau[]) |
Build 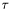 . . | |
| template<class View> | |
| bool | normalize (Space *home, ViewArray< View > &y, ViewArray< View > &x, bool &nofix) |
| Performing normalization on the views in y. | |
| template<class View> | |
| bool | perm_bc (Space *home, int tau[], SccComponent sinfo[], int scclist[], ViewArray< View > &x, ViewArray< View > &z, bool &crossingedge, bool &nofix) |
| Bounds consistency on the permutation views. | |
| template<class View, bool Perm> | |
| ExecStatus | bounds_propagation (Space *home, Propagator *p, ViewArray< View > &x, ViewArray< View > &y, ViewArray< View > &z, bool &repairpass, bool &nofix, bool &match_fixed) |
| Perform bounds consistent sortedness propagation. | |
| template<class View, bool Perm> | |
| bool | check_subsumption (ViewArray< View > &x, ViewArray< View > &y, ViewArray< View > &z, bool &subsumed, int &dropfst) |
| Subsumption test. | |
| template<class View, bool Perm> | |
| bool | array_assigned (Space *home, ViewArray< View > &x, ViewArray< View > &y, ViewArray< View > &z, bool &subsumed, bool &match_fixed, bool &, bool &noperm_bc) |
| Check for assignment of a variable array. | |
| template<class View> | |
| bool | channel (Space *home, ViewArray< View > &x, ViewArray< View > &y, ViewArray< View > &z, bool &nofix) |
| Channel between x, y and z. | |
Function Documentation
| bool Gecode::Int::Sorted::glover | ( | ViewArray< View > & | x, | |
| ViewArray< View > & | y, | |||
| int | tau[], | |||
| int | phi[], | |||
| OfflineMinItem | sequence[], | |||
| int | vertices[] | |||
| ) | [inline] |
Glover's maximum matching in a bipartite graph.
Compute a matching in the bipartite convex intersection graph with one partition containing the x views and the other containing the y views. The algorithm works with an implicit array structure of the intersection graph.
Union-Find Implementation of F.Glover's matching algorithm.
The idea is to mimick a priority queue storing x-indices ![$[i_0,\dots, i_{n-1}]$](form_206.png) , s.t. the upper domain bounds are sorted
, s.t. the upper domain bounds are sorted 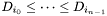 where
where 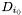 is the top element
is the top element
Definition at line 59 of file matching.icc.
| bool Gecode::Int::Sorted::revglover | ( | ViewArray< View > & | x, | |
| ViewArray< View > & | y, | |||
| int | tau[], | |||
| int | phiprime[], | |||
| OfflineMinItem | sequence[], | |||
| int | vertices[] | |||
| ) | [inline] |
| void Gecode::Int::Sorted::computesccs | ( | ViewArray< View > & | x, | |
| ViewArray< View > & | y, | |||
| int | phi[], | |||
| SccComponent | sinfo[], | |||
| int | scclist[] | |||
| ) | [inline] |
Compute the sccs of the oriented intersection-graph.
An y-node 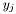 and its corresponding matching mate
and its corresponding matching mate 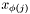 form the smallest possible scc, since both edges
form the smallest possible scc, since both edges 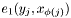 and
and 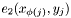 are both contained in the oriented intersection graph.
are both contained in the oriented intersection graph.
Hence a scc containg more than two nodes is represented as an array of SccComponent entries, ![$[ y_{j_0},x_{\phi(j_0)},\dots,y_{j_k},x_{\phi(j_k)}]$](form_213.png) .
.
Parameters scclist ~ resulting sccs
Definition at line 58 of file narrowing.icc.
| bool Gecode::Int::Sorted::narrow_domx | ( | Space * | home, | |
| ViewArray< View > & | x, | |||
| ViewArray< View > & | y, | |||
| ViewArray< View > & | z, | |||
| int | tau[], | |||
| int | [], | |||
| int | scclist[], | |||
| SccComponent | sinfo[], | |||
| bool & | nofix | |||
| ) | [inline] |
Narrowing the domains of the x variables.
Due to the correspondance between perfect matchings in the "reduced" intersection graph of x and y views and feasible assignments for the sorted constraint the new domain bounds for views in x are computed as
- lower bounds:
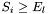 where
where 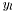 is the leftmost neighbour of
is the leftmost neighbour of 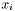
- upper bounds:
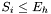 where
where 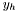 is the rightmost neighbour of
is the rightmost neighbour of 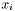
Definition at line 133 of file narrowing.icc.
| bool Gecode::Int::Sorted::narrow_domy | ( | Space * | home, | |
| ViewArray< View > & | x, | |||
| ViewArray< View > & | y, | |||
| int | phi[], | |||
| int | phiprime[], | |||
| bool & | nofix | |||
| ) | [inline] |
Narrowing the domains of the y views.
analogously to the x views we take
- for the upper bounds the matching
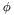 computed in glover and compute the new upper bound by
computed in glover and compute the new upper bound by 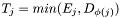
- for the lower bounds the matching
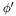 computed in revglover and update the new lower bound by
computed in revglover and update the new lower bound by 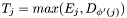
Definition at line 225 of file narrowing.icc.
| void Gecode::Int::Sorted::sort_sigma | ( | ViewArray< View > & | x, | |
| ViewArray< View > & | z | |||
| ) | [inline] |
| void Gecode::Int::Sorted::sort_tau | ( | ViewArray< View > & | x, | |
| ViewArray< View > & | z, | |||
| int | tau[] | |||
| ) | [inline] |
| bool Gecode::Int::Sorted::normalize | ( | Space * | home, | |
| ViewArray< View > & | y, | |||
| ViewArray< View > & | x, | |||
| bool & | nofix | |||
| ) | [inline] |
| bool Gecode::Int::Sorted::perm_bc | ( | Space * | home, | |
| int | tau[], | |||
| SccComponent | sinfo[], | |||
| int | scclist[], | |||
| ViewArray< View > & | x, | |||
| ViewArray< View > & | z, | |||
| bool & | crossingedge, | |||
| bool & | nofix | |||
| ) | [inline] |
Bounds consistency on the permutation views.
Check, whether the permutation view are bounds consistent. This function tests, whether there are "crossing edges", i.e. whether the current domains permit matchings between unsorted views x and the sorted variables y violating the property that y is sorted.
| ExecStatus Gecode::Int::Sorted::bounds_propagation | ( | Space * | home, | |
| Propagator * | p, | |||
| ViewArray< View > & | x, | |||
| ViewArray< View > & | y, | |||
| ViewArray< View > & | z, | |||
| bool & | repairpass, | |||
| bool & | nofix, | |||
| bool & | match_fixed | |||
| ) | [inline] |
Perform bounds consistent sortedness propagation.
Implements the propagation algorithm for Sorted::Sorted and is provided as seperate function, because a second pass of the propagation algorithm is needed in order to achieve idempotency in case explicit permutation variables are provided.
If Perm is true, permutation variables form the third argument which implies additional inferences, consistency check on the permutation variables and eventually a second pass of the propagation algorithm. Otherwise, the algorithm does not take care of the permutation variables resulting in a better performance.
Definition at line 77 of file propagate.icc.
| bool Gecode::Int::Sorted::check_subsumption | ( | ViewArray< View > & | x, | |
| ViewArray< View > & | y, | |||
| ViewArray< View > & | z, | |||
| bool & | subsumed, | |||
| int & | dropfst | |||
| ) | [inline] |
Subsumption test.
The propagator for sorted is subsumed if all variables of the ViewArrays x, y and z are determined and the constraint holds. In addition to the subsumption test check_subsumption determines, whether we can reduce the orginial problem to a smaller one, by dropping already matched variables.
Definition at line 82 of file sortsup.icc.
| bool Gecode::Int::Sorted::array_assigned | ( | Space * | home, | |
| ViewArray< View > & | x, | |||
| ViewArray< View > & | y, | |||
| ViewArray< View > & | z, | |||
| bool & | subsumed, | |||
| bool & | match_fixed, | |||
| bool & | , | |||
| bool & | noperm_bc | |||
| ) | [inline] |
Check for assignment of a variable array.
Check whether one of the argument arrays is completely assigned and udpates the other array respectively.
Definition at line 382 of file sortsup.icc.
| bool Gecode::Int::Sorted::channel | ( | Space * | home, | |
| ViewArray< View > & | x, | |||
| ViewArray< View > & | y, | |||
| ViewArray< View > & | z, | |||
| bool & | nofix | |||
| ) | [inline] |
Channel between x, y and z.
Keep variables consisting by channeling information
Definition at line 493 of file sortsup.icc.

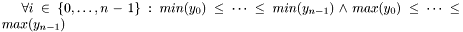 holds.
holds.