Generated on Mon Aug 25 11:35:47 2008 for Gecode by doxygen 1.5.6

Element constraints
[Using finite integer sets]

Detailed Description

An element constraint selects zero, one or more elements out of a sequence. We write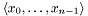 $ \langle x_0,\dots, x_{n-1} \rangle $ for the sequence, and $ [y] $ for the index variable.

Set element constraints are closely related to the element constraint on finite domain variables.


Functions

void Gecode::elementsUnion (Space *home, const SetVarArgs &x, SetVar y, SetVar z)
 Post propagator for $ z=\bigcup\langle x_0,\dots,x_{n-1}\rangle[y] $.
void Gecode::elementsUnion (Space *home, const IntSetArgs &s, SetVar y, SetVar z)
 Post propagator for $ z=\bigcup\langle s_0,\dots,s_{n-1}\rangle[y] $.
void Gecode::elementsInter (Space *home, const SetVarArgs &x, SetVar y, SetVar z)
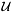 Post propagator for $ z=\bigcap\langle x_0,\dots,x_{n-1}\rangle[y] $ using $ \mathcal{U} $ as universe.
void Gecode::elementsInter (Space *home, const SetVarArgs &x, SetVar y, SetVar z, const IntSet &u)
 Post propagator for $ z=\bigcap\langle x_0,\dots,x_{n-1}\rangle[y] $ using u as universe.
void Gecode::elementsDisjoint (Space *home, const SetVarArgs &x, SetVar y)
 Post propagator for $ \parallel\langle x_0,\dots,x_{n-1}\rangle[y] $.
void Gecode::element (Space *home, const SetVarArgs &x, IntVar y, SetVar z)
 Post propagator for $ z=\langle x_0,\dots,x_{n-1}\rangle[y] $.
void Gecode::element (Space *home, const IntSetArgs &s, IntVar y, SetVar z)
 Post propagator for $ z=\langle s_0,\dots,s_{n-1}\rangle[y] $.

Function Documentation

void Gecode::elementsUnion ( Space *  home,
const SetVarArgs &  x,
SetVar  y,
SetVar  z 
)

Post propagator for $ z=\bigcup\langle x_0,\dots,x_{n-1}\rangle[y] $.

If y is the empty set, z will also be constrained to be empty (as an empty union is empty). The indices for s start at 0.

Definition at line 47 of file element.cc.

void Gecode::elementsUnion ( Space *  home,
const IntSetArgs &  s,
SetVar  y,
SetVar  z 
)

Post propagator for $ z=\bigcup\langle s_0,\dots,s_{n-1}\rangle[y] $.

If y is the empty set, z will also be constrained to be empty (as an empty union is empty). The indices for s start at 0.

Definition at line 56 of file element.cc.

void Gecode::elementsInter ( Space *  home,
const SetVarArgs &  x,
SetVar  y,
SetVar  z 
)

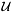Post propagator for $ z=\bigcap\langle x_0,\dots,x_{n-1}\rangle[y] $ using $ \mathcal{U} $ as universe.

If y is empty, z will be constrained to be the universe 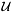$ \mathcal{U} $ (as an empty intersection is the universe). The indices for s start at 0.

Definition at line 67 of file element.cc.

void Gecode::elementsInter ( Space *  home,
const SetVarArgs &  x,
SetVar  y,
SetVar  z,
const IntSet &  u 
)

Post propagator for $ z=\bigcap\langle x_0,\dots,x_{n-1}\rangle[y] $ using u as universe.

If y is empty, z will be constrained to be the given universe u (as an empty intersection is the universe). The indices for s start at 0.

Definition at line 78 of file element.cc.

void Gecode::elementsDisjoint ( Space *  home,
const SetVarArgs &  x,
SetVar  y 
)

Post propagator for $ \parallel\langle x_0,\dots,x_{n-1}\rangle[y] $.

Definition at line 88 of file element.cc.

void Gecode::element ( Space *  home,
const SetVarArgs &  x,
IntVar  y,
SetVar  z 
)

Post propagator for $ z=\langle x_0,\dots,x_{n-1}\rangle[y] $.

The indices for s start at 0.

Definition at line 95 of file element.cc.

void Gecode::element ( Space *  home,
const IntSetArgs &  s,
IntVar  y,
SetVar  z 
)

Post propagator for $ z=\langle s_0,\dots,s_{n-1}\rangle[y] $.

The indices for s start at 0.

Definition at line 107 of file element.cc.