Simple relation constraints over integer variables
[Using integer variables and constraints]
Functions | |
| void | Gecode::rel (Home home, IntVar x0, IntRelType irt, IntVar x1, IntPropLevel ipl=IPL_DEF) |
Post propagator for 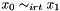 . . | |
| void | Gecode::rel (Home home, const IntVarArgs &x, IntRelType irt, IntVar y, IntPropLevel ipl=IPL_DEF) |
Post propagator for 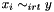 for all for all 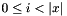 . . | |
| void | Gecode::rel (Home home, IntVar x, IntRelType irt, int c, IntPropLevel ipl=IPL_DEF) |
Propagates 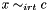 . . | |
| void | Gecode::rel (Home home, const IntVarArgs &x, IntRelType irt, int c, IntPropLevel ipl=IPL_DEF) |
Propagates 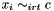 for all for all 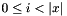 . . | |
| void | Gecode::rel (Home home, IntVar x0, IntRelType irt, IntVar x1, Reify r, IntPropLevel ipl=IPL_DEF) |
Post propagator for 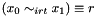 . . | |
| void | Gecode::rel (Home home, IntVar x, IntRelType irt, int c, Reify r, IntPropLevel ipl=IPL_DEF) |
Post propagator for 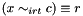 . . | |
| void | Gecode::rel (Home home, const IntVarArgs &x, IntRelType irt, IntPropLevel ipl=IPL_DEF) |
| Post propagator for relation among elements in x. | |
| void | Gecode::rel (Home home, const IntVarArgs &x, IntRelType irt, const IntVarArgs &y, IntPropLevel ipl=IPL_DEF) |
| Post propagator for relation between x and y. | |
| void | Gecode::rel (Home home, const IntVarArgs &x, IntRelType irt, const IntArgs &y, IntPropLevel ipl=IPL_DEF) |
| Post propagator for relation between x and y. | |
| void | Gecode::rel (Home home, const IntArgs &x, IntRelType irt, const IntVarArgs &y, IntPropLevel ipl=IPL_DEF) |
| Post propagator for relation between x and y. | |
Function Documentation
| void Gecode::rel | ( | Home | home, | |
| IntVar | x0, | |||
| IntRelType | irt, | |||
| IntVar | x1, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 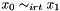 .
.
Supports both bounds (ipl = IPL_BND) and domain consistency (ipl = IPL_DOM, default).
| void Gecode::rel | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| IntVar | y, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 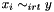 for all
for all 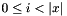 .
.
Supports both bounds (ipl = IPL_BND) and domain consistency (ipl = IPL_DOM, default).
| void Gecode::rel | ( | Home | home, | |
| IntVar | x0, | |||
| IntRelType | irt, | |||
| int | n, | |||
| IntPropLevel | ||||
| ) |
Propagates 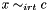 .
.
| void Gecode::rel | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| int | n, | |||
| IntPropLevel | ||||
| ) |
Propagates 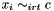 for all
for all 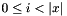 .
.
| void Gecode::rel | ( | Home | home, | |
| IntVar | x0, | |||
| IntRelType | irt, | |||
| IntVar | x1, | |||
| Reify | r, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 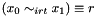 .
.
Supports both bounds (ipl = IPL_BND) and domain consistency (ipl = IPL_DOM, default).
| void Gecode::rel | ( | Home | home, | |
| IntVar | x, | |||
| IntRelType | irt, | |||
| int | c, | |||
| Reify | r, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 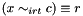 .
.
Supports both bounds (ipl = IPL_BND) and domain consistency (ipl = IPL_DOM, default).
| void Gecode::rel | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for relation among elements in x.
States that the elements of x are in the following relation:
- if r = IRT_LE, r = IRT_LQ, r = IRT_GR, or r = IRT_GQ, then the elements of x are ordered with respect to r. Supports domain consistency (ipl = IPL_DOM, default).
- if r = IRT_EQ, then all elements of x must be equal. Supports both bounds (ipl = IPL_BND) and domain consistency (ipl = IPL_DOM, default).
- if r = IRT_NQ, then not all elements of x must be equal. Supports domain consistency (ipl = IPL_DOM, default).
| void Gecode::rel | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| const IntVarArgs & | y, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for relation between x and y.
Note that for the inequality relations this corresponds to the lexical order between x and y.
Supports both bounds (ipl = IPL_BND) and domain consistency (ipl = IPL_DOM, default).
Note that the constraint is also defined if x and y are of different size. That means that if x and y are of different size, then if r = IRT_EQ the constraint is false and if r = IRT_NQ the constraint is subsumed.
| void Gecode::rel | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| const IntArgs & | y, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for relation between x and y.
Note that for the inequality relations this corresponds to the lexical order between x and y.
Supports domain consistency.
Note that the constraint is also defined if x and y are of different size. That means that if x and y are of different size, then if r = IRT_EQ the constraint is false and if r = IRT_NQ the constraint is subsumed.
| void Gecode::rel | ( | Home | home, | |
| const IntArgs & | x, | |||
| IntRelType | irt, | |||
| const IntVarArgs & | y, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for relation between x and y.
Note that for the inequality relations this corresponds to the lexical order between x and y.
Supports domain consistency.
Note that the constraint is also defined if x and y are of different size. That means that if x and y are of different size, then if r = IRT_EQ the constraint is false and if r = IRT_NQ the constraint is subsumed.
