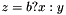Simple relation constraints over Boolean variables
[Using integer variables and constraints]
Functions | |
| void | Gecode::rel (Home home, BoolVar x0, IntRelType irt, BoolVar x1, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for 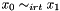 . . | |
| void | Gecode::rel (Home home, BoolVar x0, IntRelType irt, BoolVar x1, Reify r, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for 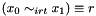 . . | |
| void | Gecode::rel (Home home, const BoolVarArgs &x, IntRelType irt, BoolVar y, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for 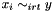 for all for all 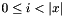 . . | |
| void | Gecode::rel (Home home, BoolVar x, IntRelType irt, int n, IntPropLevel ipl=IPL_DEF) |
Propagates 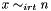 . . | |
| void | Gecode::rel (Home home, BoolVar x, IntRelType irt, int n, Reify r, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for 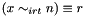 . . | |
| void | Gecode::rel (Home home, const BoolVarArgs &x, IntRelType irt, int n, IntPropLevel ipl=IPL_DEF) |
Propagates 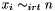 for all for all 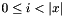 . . | |
| void | Gecode::rel (Home home, const BoolVarArgs &x, IntRelType irt, const BoolVarArgs &y, IntPropLevel ipl=IPL_DEF) |
| Post domain consistent propagator for relation between x and y. | |
| void | Gecode::rel (Home home, const BoolVarArgs &x, IntRelType irt, const IntArgs &y, IntPropLevel ipl=IPL_DEF) |
| Post domain consistent propagator for relation between x and y. | |
| void | Gecode::rel (Home home, const IntArgs &x, IntRelType irt, const BoolVarArgs &y, IntPropLevel ipl=IPL_DEF) |
| Post domain consistent propagator for relation between x and y. | |
| void | Gecode::rel (Home home, const BoolVarArgs &x, IntRelType irt, IntPropLevel ipl=IPL_DEF) |
| Post domain consistent propagator for relation between elements in x. | |
| void | Gecode::rel (Home home, BoolVar x0, BoolOpType o, BoolVar x1, BoolVar x2, IntPropLevel ipl=IPL_DEF) |
| Post domain consistent propagator for Boolean operation on x0 and x1. | |
| void | Gecode::rel (Home home, BoolVar x0, BoolOpType o, BoolVar x1, int n, IntPropLevel ipl=IPL_DEF) |
| Post domain consistent propagator for Boolean operation on x0 and x1. | |
| void | Gecode::rel (Home home, BoolOpType o, const BoolVarArgs &x, BoolVar y, IntPropLevel ipl=IPL_DEF) |
| Post domain consistent propagator for Boolean operation on x. | |
| void | Gecode::rel (Home home, BoolOpType o, const BoolVarArgs &x, int n, IntPropLevel ipl=IPL_DEF) |
| Post domain consistent propagator for Boolean operation on x. | |
| void | Gecode::clause (Home home, BoolOpType o, const BoolVarArgs &x, const BoolVarArgs &y, BoolVar z, IntPropLevel ipl=IPL_DEF) |
| Post domain consistent propagator for Boolean clause with positive variables x and negative variables y. | |
| void | Gecode::clause (Home home, BoolOpType o, const BoolVarArgs &x, const BoolVarArgs &y, int n, IntPropLevel ipl=IPL_DEF) |
| Post domain consistent propagator for Boolean clause with positive variables x and negative variables y. | |
| void | Gecode::ite (Home home, BoolVar b, IntVar x, IntVar y, IntVar z, IntPropLevel ipl=IPL_DEF) |
| Post propagator for if-then-else constraint. | |
| void | Gecode::ite (Home home, BoolVar b, BoolVar x, BoolVar y, BoolVar z, IntPropLevel ipl=IPL_DEF) |
| Post propagator for if-then-else constraint. | |
Function Documentation
| void Gecode::rel | ( | Home | home, | |
| BoolVar | x0, | |||
| IntRelType | irt, | |||
| BoolVar | x1, | |||
| IntPropLevel | ||||
| ) |
Post domain consistent propagator for 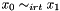 .
.
| void Gecode::rel | ( | Home | home, | |
| BoolVar | x0, | |||
| IntRelType | irt, | |||
| BoolVar | x1, | |||
| Reify | r, | |||
| IntPropLevel | ||||
| ) |
Post domain consistent propagator for 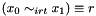 .
.
| void Gecode::rel | ( | Home | home, | |
| const BoolVarArgs & | x, | |||
| IntRelType | irt, | |||
| BoolVar | y, | |||
| IntPropLevel | ||||
| ) |
Post domain consistent propagator for 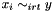 for all
for all 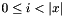 .
.
| void Gecode::rel | ( | Home | home, | |
| BoolVar | x, | |||
| IntRelType | irt, | |||
| int | n, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Propagates 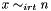 .
.
Throws an exception of type Int::NotZeroOne, if n is neither 0 or 1.
| void Gecode::rel | ( | Home | home, | |
| BoolVar | x, | |||
| IntRelType | irt, | |||
| int | n, | |||
| Reify | r, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for 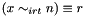 .
.
Throws an exception of type Int::NotZeroOne, if n is neither 0 or 1.
| void Gecode::rel | ( | Home | home, | |
| const BoolVarArgs & | x, | |||
| IntRelType | irt, | |||
| int | n, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Propagates 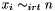 for all
for all 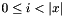 .
.
Throws an exception of type Int::NotZeroOne, if n is neither 0 or 1.
| void Gecode::rel | ( | Home | home, | |
| const BoolVarArgs & | x, | |||
| IntRelType | irt, | |||
| const BoolVarArgs & | y, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for relation between x and y.
Note that for the inequality relations this corresponds to the lexical order between x and y.
Note that the constraint is also defined if x and y are of different size. That means that if x and y are of different size, then if r = IRT_EQ the constraint is false and if r = IRT_NQ the constraint is subsumed.
| void Gecode::rel | ( | Home | home, | |
| const BoolVarArgs & | x, | |||
| IntRelType | irt, | |||
| const IntArgs & | y, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for relation between x and y.
Note that for the inequality relations this corresponds to the lexical order between x and y.
Note that the constraint is also defined if x and y are of different size. That means that if x and y are of different size, then if r = IRT_EQ the constraint is false and if r = IRT_NQ the constraint is subsumed.
| void Gecode::rel | ( | Home | home, | |
| const IntArgs & | x, | |||
| IntRelType | irt, | |||
| const BoolVarArgs & | y, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for relation between x and y.
Note that for the inequality relations this corresponds to the lexical order between x and y.
Note that the constraint is also defined if x and y are of different size. That means that if x and y are of different size, then if r = IRT_EQ the constraint is false and if r = IRT_NQ the constraint is subsumed.
| void Gecode::rel | ( | Home | home, | |
| const BoolVarArgs & | x, | |||
| IntRelType | irt, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for relation between elements in x.
States that the elements of x are in the following relation:
- if r = IRT_LE, r = IRT_LQ, r = IRT_GR, or r = IRT_GQ, then the elements of x are ordered with respect to r.
- if r = IRT_EQ, then all elements of x must be equal.
- if r = IRT_NQ, then not all elements of x must be equal.
| void Gecode::rel | ( | Home | home, | |
| BoolVar | x0, | |||
| BoolOpType | o, | |||
| BoolVar | x1, | |||
| BoolVar | x2, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for Boolean operation on x0 and x1.
Posts propagator for 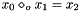
| void Gecode::rel | ( | Home | home, | |
| BoolVar | x0, | |||
| BoolOpType | o, | |||
| BoolVar | x1, | |||
| int | n, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for Boolean operation on x0 and x1.
Posts propagator for 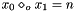
Throws an exception of type Int::NotZeroOne, if n is neither 0 or 1.
| void Gecode::rel | ( | Home | home, | |
| BoolOpType | o, | |||
| const BoolVarArgs & | x, | |||
| BoolVar | y, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for Boolean operation on x.
Posts propagator for 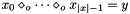
Throws an exception of type Int::TooFewArguments, if 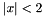 and o is BOT_IMP, BOT_EQV, or BOT_XOR.
and o is BOT_IMP, BOT_EQV, or BOT_XOR.
| void Gecode::rel | ( | Home | home, | |
| BoolOpType | o, | |||
| const BoolVarArgs & | x, | |||
| int | n, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for Boolean operation on x.
Posts propagator for 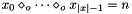
Throws an exception of type Int::NotZeroOne, if n is neither 0 or 1.
Throws an exception of type Int::TooFewArguments, if 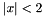 and o is BOT_IMP, BOT_EQV, or BOT_XOR.
and o is BOT_IMP, BOT_EQV, or BOT_XOR.
| void Gecode::clause | ( | Home | home, | |
| BoolOpType | o, | |||
| const BoolVarArgs & | x, | |||
| const BoolVarArgs & | y, | |||
| BoolVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for Boolean clause with positive variables x and negative variables y.
Posts propagator for 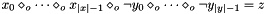
Throws an exception of type Int::IllegalOperation, if o is different from BOT_AND or BOT_OR.
| void Gecode::clause | ( | Home | home, | |
| BoolOpType | o, | |||
| const BoolVarArgs & | x, | |||
| const BoolVarArgs & | y, | |||
| int | n, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for Boolean clause with positive variables x and negative variables y.
Posts propagator for 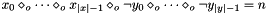
Throws an exception of type Int::NotZeroOne, if n is neither 0 or 1.
Throws an exception of type Int::IllegalOperation, if o is different from BOT_AND or BOT_OR.
| void Gecode::ite | ( | Home | home, | |
| BoolVar | b, | |||
| IntVar | x, | |||
| IntVar | y, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for if-then-else constraint.
Posts propagator for 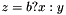
Supports both bounds (ipl = IPL_BND) and domain consistency (ipl = IPL_DOM, default).
| void Gecode::ite | ( | Home | home, | |
| BoolVar | b, | |||
| BoolVar | x, | |||
| BoolVar | y, | |||
| BoolVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for if-then-else constraint.
Posts propagator for