Element constraints
[Using integer variables and constraints]
Typedefs | |
| typedef SharedArray< int > | Gecode::IntSharedArray |
| Arrays of integers that can be shared among several element constraints. | |
Functions | |
| void | Gecode::element (Home home, IntSharedArray n, IntVar x0, IntVar x1, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for  . . | |
| void | Gecode::element (Home home, IntSharedArray n, IntVar x0, BoolVar x1, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for  . . | |
| void | Gecode::element (Home home, IntSharedArray n, IntVar x0, int x1, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for  . . | |
| void | Gecode::element (Home home, const IntVarArgs &x, IntVar y0, IntVar y1, IntPropLevel ipl=IPL_DEF) |
Post propagator for 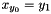 . . | |
| void | Gecode::element (Home home, const IntVarArgs &x, IntVar y0, int y1, IntPropLevel ipl=IPL_DEF) |
Post propagator for 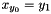 . . | |
| void | Gecode::element (Home home, const BoolVarArgs &x, IntVar y0, BoolVar y1, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for 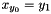 . . | |
| void | Gecode::element (Home home, const BoolVarArgs &x, IntVar y0, int y1, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for 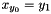 . . | |
| void | Gecode::element (Home home, IntSharedArray a, IntVar x, int w, IntVar y, int h, IntVar z, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for 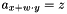 . . | |
| void | Gecode::element (Home home, IntSharedArray a, IntVar x, int w, IntVar y, int h, BoolVar z, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for 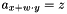 . . | |
| void | Gecode::element (Home home, const IntVarArgs &a, IntVar x, int w, IntVar y, int h, IntVar z, IntPropLevel ipl=IPL_DEF) |
Post propagator for 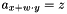 . . | |
| void | Gecode::element (Home home, const BoolVarArgs &a, IntVar x, int w, IntVar y, int h, BoolVar z, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for 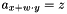 . . | |
Typedef Documentation
| typedef SharedArray<int> Gecode::IntSharedArray |
Function Documentation
| void Gecode::element | ( | Home | home, | |
| IntSharedArray | n, | |||
| IntVar | x0, | |||
| IntVar | x1, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for  .
.
Throws an exception of type Int::OutOfLimits, if the integers in n exceed the limits in Int::Limits.
| void Gecode::element | ( | Home | home, | |
| IntSharedArray | n, | |||
| IntVar | x0, | |||
| BoolVar | x1, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for  .
.
Throws an exception of type Int::OutOfLimits, if the integers in n exceed the limits in Int::Limits.
| void Gecode::element | ( | Home | home, | |
| IntSharedArray | n, | |||
| IntVar | x0, | |||
| int | x1, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for  .
.
Throws an exception of type Int::OutOfLimits, if the integers in n exceed the limits in Int::Limits.
| void Gecode::element | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntVar | y0, | |||
| IntVar | y1, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 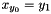 .
.
Supports both bounds (ipl = IPL_BND) and domain consistency (ipl = IPL_DOM, default).
| void Gecode::element | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntVar | y0, | |||
| int | y1, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 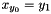 .
.
Supports both bounds (ipl = IPL_BND) and domain consistency (ipl = IPL_DOM, default).
| void Gecode::element | ( | Home | home, | |
| const BoolVarArgs & | c, | |||
| IntVar | x0, | |||
| BoolVar | x1, | |||
| IntPropLevel | ||||
| ) |
Post domain consistent propagator for 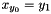 .
.
| void Gecode::element | ( | Home | home, | |
| const BoolVarArgs & | c, | |||
| IntVar | x0, | |||
| int | x1, | |||
| IntPropLevel | ||||
| ) |
Post domain consistent propagator for 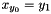 .
.
| void Gecode::element | ( | Home | home, | |
| IntSharedArray | a, | |||
| IntVar | x, | |||
| int | w, | |||
| IntVar | y, | |||
| int | h, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for 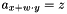 .
.
If a is regarded as a two-dimensional array in row-major order of width w and height h, then z is constrained to be the element in column x and row y.
Throws an exception of type Int::OutOfLimits, if the integers in n exceed the limits in Int::Limits.
Throws an exception of type Int::ArgumentSizeMismatch, if 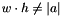 .
.
| void Gecode::element | ( | Home | home, | |
| IntSharedArray | a, | |||
| IntVar | x, | |||
| int | w, | |||
| IntVar | y, | |||
| int | h, | |||
| BoolVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for 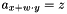 .
.
If a is regarded as a two-dimensional array in row-major order of width w and height h, then z is constrained to be the element in column x and row y.
Throws an exception of type Int::OutOfLimits, if the integers in n exceed the limits in Int::Limits.
Throws an exception of type Int::ArgumentSizeMismatch, if 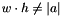 .
.
| void Gecode::element | ( | Home | home, | |
| const IntVarArgs & | a, | |||
| IntVar | x, | |||
| int | w, | |||
| IntVar | y, | |||
| int | h, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 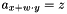 .
.
If a is regarded as a two-dimensional array in row-major order of width w and height h, then z is constrained to be the element in column x and row y.
Supports both bounds (ipl = IPL_BND) and domain consistency (ipl = IPL_DOM, default).
Throws an exception of type Int::OutOfLimits, if the integers in n exceed the limits in Int::Limits.
Throws an exception of type Int::ArgumentSizeMismatch, if 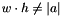 .
.
| void Gecode::element | ( | Home | home, | |
| const BoolVarArgs & | a, | |||
| IntVar | x, | |||
| int | w, | |||
| IntVar | y, | |||
| int | h, | |||
| BoolVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post domain consistent propagator for 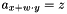 .
.
If a is regarded as a two-dimensional array in row-major order of width w and height h, then z is constrained to be the element in column x and row y.
Throws an exception of type Int::OutOfLimits, if the integers in n exceed the limits in Int::Limits.
Throws an exception of type Int::ArgumentSizeMismatch, if 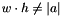 .
.
