Arithmetic constraints
[Using integer variables and constraints]
Functions | |
| void | Gecode::min (Home home, IntVar x0, IntVar x1, IntVar x2, IntPropLevel ipl=IPL_DEF) |
Post propagator for 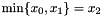 . . | |
| void | Gecode::min (Home home, const IntVarArgs &x, IntVar y, IntPropLevel ipl=IPL_DEF) |
Post propagator for 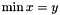 . . | |
| void | Gecode::max (Home home, IntVar x0, IntVar x1, IntVar x2, IntPropLevel ipl=IPL_DEF) |
Post propagator for 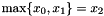 . . | |
| void | Gecode::max (Home home, const IntVarArgs &x, IntVar y, IntPropLevel ipl=IPL_DEF) |
Post propagator for 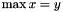 . . | |
| void | Gecode::argmin (Home home, const IntVarArgs &x, IntVar y, bool tiebreak=true, IntPropLevel ipl=IPL_DEF) |
Post propagator for 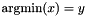 . . | |
| void | Gecode::argmin (Home home, const IntVarArgs &x, int o, IntVar y, bool tiebreak=true, IntPropLevel ipl=IPL_DEF) |
Post propagator for 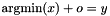 . . | |
| void | Gecode::argmax (Home home, const IntVarArgs &x, IntVar y, bool tiebreak=true, IntPropLevel ipl=IPL_DEF) |
Post propagator for 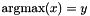 . . | |
| void | Gecode::argmax (Home home, const IntVarArgs &x, int o, IntVar y, bool tiebreak=true, IntPropLevel ipl=IPL_DEF) |
Post propagator for 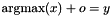 . . | |
| void | Gecode::argmin (Home home, const BoolVarArgs &x, IntVar y, bool tiebreak=true, IntPropLevel ipl=IPL_DEF) |
Post propagator for 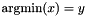 . . | |
| void | Gecode::argmin (Home home, const BoolVarArgs &x, int o, IntVar y, bool tiebreak=true, IntPropLevel ipl=IPL_DEF) |
Post propagator for 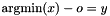 . . | |
| void | Gecode::argmax (Home home, const BoolVarArgs &x, IntVar y, bool tiebreak=true, IntPropLevel ipl=IPL_DEF) |
Post propagator for 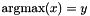 . . | |
| void | Gecode::argmax (Home home, const BoolVarArgs &x, int o, IntVar y, bool tiebreak=true, IntPropLevel ipl=IPL_DEF) |
Post propagator for 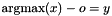 . . | |
| void | Gecode::abs (Home home, IntVar x0, IntVar x1, IntPropLevel ipl=IPL_DEF) |
Post propagator for 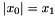 . . | |
| void | Gecode::mult (Home home, IntVar x0, IntVar x1, IntVar x2, IntPropLevel ipl=IPL_DEF) |
Post propagator for 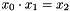 . . | |
| void | Gecode::divmod (Home home, IntVar x0, IntVar x1, IntVar x2, IntVar x3, IntPropLevel ipl=IPL_DEF) |
Post propagator for 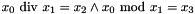 . . | |
| void | Gecode::div (Home home, IntVar x0, IntVar x1, IntVar x2, IntPropLevel ipl=IPL_DEF) |
Post propagator for 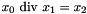 . . | |
| void | Gecode::mod (Home home, IntVar x0, IntVar x1, IntVar x2, IntPropLevel ipl=IPL_DEF) |
Post propagator for 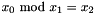 . . | |
| void | Gecode::sqr (Home home, IntVar x0, IntVar x1, IntPropLevel ipl=IPL_DEF) |
Post propagator for 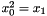 . . | |
| void | Gecode::sqrt (Home home, IntVar x0, IntVar x1, IntPropLevel ipl=IPL_DEF) |
Post propagator for 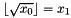 . . | |
| void | Gecode::pow (Home home, IntVar x0, int n, IntVar x1, IntPropLevel ipl=IPL_DEF) |
Post propagator for 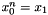 . . | |
| void | Gecode::nroot (Home home, IntVar x0, int n, IntVar x1, IntPropLevel ipl=IPL_DEF) |
Post propagator for ![$\lfloor\sqrt[n]{x_0}\rfloor=x_1$](form_375.png) . . | |
Function Documentation
| void Gecode::min | ( | Home | home, | |
| IntVar | x0, | |||
| IntVar | x1, | |||
| IntVar | x2, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 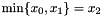 .
.
Supports both bounds consistency (ipl = IPL_BND, default) and domain consistency (ipl = IPL_DOM).
| void Gecode::min | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntVar | y, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 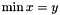 .
.
Supports both bounds consistency (ipl = IPL_BND, default) and domain consistency (ipl = IPL_DOM).
If x is empty, an exception of type Int::TooFewArguments is thrown.
| void Gecode::max | ( | Home | home, | |
| IntVar | x0, | |||
| IntVar | x1, | |||
| IntVar | x2, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 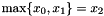 .
.
Supports both bounds consistency (ipl = IPL_BND, default) and domain consistency (ipl = IPL_DOM).
| void Gecode::max | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntVar | y, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 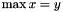 .
.
Supports both bounds consistency (ipl = IPL_BND, default) and domain consistency (ipl = IPL_DOM).
If x is empty, an exception of type Int::TooFewArguments is thrown.
| void Gecode::argmin | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntVar | y, | |||
| bool | tiebreak = true, |
|||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 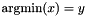 .
.
In case of ties, the smallest value for y is chosen (provided tiebreak is true).
If x is empty, an exception of type Int::TooFewArguments is thrown. If y occurs in x, an exception of type Int::ArgumentSame is thrown.
| void Gecode::argmin | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| int | o, | |||
| IntVar | y, | |||
| bool | tiebreak = true, |
|||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 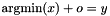 .
.
In case of ties, the smallest value for y is chosen (provided tiebreak is true).
If x is empty, an exception of type Int::TooFewArguments is thrown. If y occurs in x, an exception of type Int::ArgumentSame is thrown.
| void Gecode::argmax | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntVar | y, | |||
| bool | tiebreak = true, |
|||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 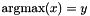 .
.
In case of ties, the smallest value for y is chosen (provided tiebreak is true).
If x is empty, an exception of type Int::TooFewArguments is thrown. If y occurs in x, an exception of type Int::ArgumentSame is thrown.
| void Gecode::argmax | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| int | o, | |||
| IntVar | y, | |||
| bool | tiebreak = true, |
|||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 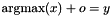 .
.
In case of ties, the smallest value for y is chosen (provided tiebreak is true).
If x is empty, an exception of type Int::TooFewArguments is thrown. If y occurs in x, an exception of type Int::ArgumentSame is thrown.
| void Gecode::argmin | ( | Home | home, | |
| const BoolVarArgs & | x, | |||
| IntVar | y, | |||
| bool | tiebreak = true, |
|||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 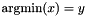 .
.
In case of ties, the smallest value for y is chosen (provided tiebreak is true).
If x is empty, an exception of type Int::TooFewArguments is thrown. If y occurs in x, an exception of type Int::ArgumentSame is thrown.
| void Gecode::argmin | ( | Home | home, | |
| const BoolVarArgs & | x, | |||
| int | o, | |||
| IntVar | y, | |||
| bool | tiebreak = true, |
|||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 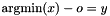 .
.
In case of ties, the smallest value for y is chosen (provided tiebreak is true).
If x is empty, an exception of type Int::TooFewArguments is thrown. If y occurs in x, an exception of type Int::ArgumentSame is thrown.
| void Gecode::argmax | ( | Home | home, | |
| const BoolVarArgs & | x, | |||
| IntVar | y, | |||
| bool | tiebreak = true, |
|||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 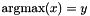 .
.
In case of ties, the smallest value for y is chosen (provided tiebreak is true).
If x is empty, an exception of type Int::TooFewArguments is thrown. If y occurs in x, an exception of type Int::ArgumentSame is thrown.
| void Gecode::argmax | ( | Home | home, | |
| const BoolVarArgs & | x, | |||
| int | o, | |||
| IntVar | y, | |||
| bool | tiebreak = true, |
|||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 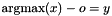 .
.
In case of ties, the smallest value for y is chosen (provided tiebreak is true).
If x is empty, an exception of type Int::TooFewArguments is thrown. If y occurs in x, an exception of type Int::ArgumentSame is thrown.
| void Gecode::abs | ( | Home | home, | |
| IntVar | x0, | |||
| IntVar | x1, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 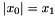 .
.
Supports both bounds consistency (ipl = IPL_BND, default) and domain consistency (ipl = IPL_DOM).
| void Gecode::mult | ( | Home | home, | |
| IntVar | x0, | |||
| IntVar | x1, | |||
| IntVar | x2, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 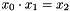 .
.
Supports both bounds consistency (ipl = IPL_BND, default) and domain consistency (ipl = IPL_DOM).
| void Gecode::divmod | ( | Home | home, | |
| IntVar | x0, | |||
| IntVar | x1, | |||
| IntVar | x2, | |||
| IntVar | x3, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 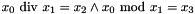 .
.
Supports bounds consistency (ipl = IPL_BND, default).
| void Gecode::div | ( | Home | home, | |
| IntVar | x0, | |||
| IntVar | x1, | |||
| IntVar | x2, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 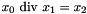 .
.
Supports bounds consistency (ipl = IPL_BND, default).
| void Gecode::mod | ( | Home | home, | |
| IntVar | x0, | |||
| IntVar | x1, | |||
| IntVar | x2, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 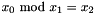 .
.
Supports bounds consistency (ipl = IPL_BND, default).
| void Gecode::sqr | ( | Home | home, | |
| IntVar | x0, | |||
| IntVar | x1, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 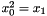 .
.
Supports both bounds consistency (ipl = IPL_BND, default) and domain consistency (ipl = IPL_DOM).
| void Gecode::sqrt | ( | Home | home, | |
| IntVar | x0, | |||
| IntVar | x1, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 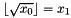 .
.
Supports both bounds consistency (ipl = IPL_BND, default) and domain consistency (ipl = IPL_DOM).
| void Gecode::pow | ( | Home | home, | |
| IntVar | x0, | |||
| int | n, | |||
| IntVar | x1, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 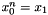 .
.
Supports both bounds consistency (ipl = IPL_BND, default) and domain consistency (ipl = IPL_DOM).
Throws an exception of type Int::OutOfLimits, if n is negative.
| void Gecode::nroot | ( | Home | home, | |
| IntVar | x0, | |||
| int | n, | |||
| IntVar | x1, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for ![$\lfloor\sqrt[n]{x_0}\rfloor=x_1$](form_375.png) .
.
Supports both bounds consistency (ipl = IPL_BND, default) and domain consistency (ipl = IPL_DOM).
Throws an exception of type Int::OutOfLimits, if n is not strictly positive.
