Pentominoes Class Reference
[Example scripts (models)]
Example: Pentominoes More...
Public Types | |
| enum | { PROPAGATION_INT, PROPAGATION_BOOLEAN } |
Choice of propagators. More... | |
| enum | { SYMMETRY_NONE, SYMMETRY_FULL } |
Choice of symmetry breaking. More... | |
Public Member Functions | |
| Pentominoes (const SizeOptions &opt) | |
| Construction of the model. | |
| Pentominoes (Pentominoes &s) | |
| Constructor for cloning s. | |
| virtual Space * | copy (void) |
| Copy space during cloning. | |
| virtual void | print (std::ostream &os) const |
| Print solution. | |
Related Functions | |
(Note that these are not member functions.) | |
| const unsigned int | n_examples |
| Number of board specifications. | |
Symmetry functions | |
These functions implement the 8 symmetries of 2D planes. The functions are templatized so that they can be used both for the pieces (defined using C-strings) and for arrays of variables. | |
| typedef void(* | tsymmfunc )(const char *, int, int, char *, int &, int &) |
| Type for tile symmetry functions. | |
| typedef void(* | bsymmfunc )(const IntVarArgs, int, int, IntVarArgs &, int &, int &) |
| Type for board symmetry functions. | |
| int | pos (int h, int w, int h1, int w1) |
| template<class CArray , class Array > | |
| void | id (CArray t1, int w1, int h1, Array t2, int &w2, int &h2) |
| Identity symmetry. | |
| template<class CArray , class Array > | |
| void | rot90 (CArray t1, int w1, int h1, Array t2, int &w2, int &h2) |
| Rotate 90 degrees. | |
| template<class CArray , class Array > | |
| void | rot180 (CArray t1, int w1, int h1, Array t2, int &w2, int &h2) |
| Rotate 180 degrees. | |
| template<class CArray , class Array > | |
| void | rot270 (CArray t1, int w1, int h1, Array t2, int &w2, int &h2) |
| Rotate 270 degrees. | |
| template<class CArray , class Array > | |
| void | flipx (CArray t1, int w1, int h1, Array t2, int &w2, int &h2) |
| Flip x-wise. | |
| template<class CArray , class Array > | |
| void | flipy (CArray t1, int w1, int h1, Array t2, int &w2, int &h2) |
| Flip y-wise. | |
| template<class CArray , class Array > | |
| void | flipd1 (CArray t1, int w1, int h1, Array t2, int &w2, int &h2) |
| Flip diagonal 1. | |
| template<class CArray , class Array > | |
| void | flipd2 (CArray t1, int w1, int h1, Array t2, int &w2, int &h2) |
| Flip diagonal 2. | |
Puzzle specifications | |
|
| |
| const TileSpec * | examples [] |
| Board specifications. | |
| const int | examples_size [] |
| Board specification sizes. | |
| static const TileSpec | puzzle0 [] |
| Small specification. | |
| static const TileSpec | puzzle1 [] |
| Standard specification. | |
| static const TileSpec | square2 [] |
| Board specifications. | |
| static const TileSpec | square3 [] |
| Board specifications. | |
| static const TileSpec | pentomino6x10 [] |
| Board specifications. | |
| static const TileSpec | pentomino5x12 [] |
| Board specifications. | |
| static const TileSpec | pentomino4x15 [] |
| Board specifications. | |
| static const TileSpec | pentomino3x20 [] |
| Board specifications. | |
| const unsigned | n_examples = sizeof(examples)/sizeof(TileSpec*) |
| Number of specifications. | |
| const TileSpec * | examples [] |
| List of specifications. | |
| const int | examples_size [] |
| Board specifications. | |
Detailed Description
Example: Pentominoes
The Problem
This example places pieces of a puzzle, where each piece is composed of a collection of squares, onto a grid. The pieces may all be rotated and flipped freely. The goal is to place all the pieces on the grid, without any overlaps. An example piece to be placed looks like
XXX X XXX
in one of its rotations.
The most famous instance of such a puzzle is the Pentominoes puzzle, where the pieces are all pieces formed by 5 four-connected squares.
The Variables
The variables for the model is the grid of squares that the pieces are placed on, where each of the variables for the squares takes the value of the number of the piece which is placed overonto it.
Placing one piece
The constraint for each piece placement uses regular expressions (and consequently the extensional constraint) for expressing placement of (rotated) pieces on the grid. Consider the simple example of placing the piece
XX X X
onto the 4 by 4 board
0123 4567 89AB CDEF
Let the variables 0-F be 0/1-variables indicating if the piece is placed on that position or not. First consider placing the piece on some location, say covering 1,2,6, and A. Then, writing the sequence of values for the variables 0-F out, we get the string 0110001000100000. This string and all other strings corresponding to placing the above piece in that particular rotation can be described using the regular expression 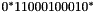 . The expression indicates that first comes some number of zeroes, then two ones in a row (covering places 1 and 2 in our example placement), then comes exactly three 0's (not covering places 3, 4, and 5), and so on. The variable number of 0's at the beginning and at the end makes the expression match any placement of the piece on the board.
. The expression indicates that first comes some number of zeroes, then two ones in a row (covering places 1 and 2 in our example placement), then comes exactly three 0's (not covering places 3, 4, and 5), and so on. The variable number of 0's at the beginning and at the end makes the expression match any placement of the piece on the board.
There is one problem with the above constraint, since it allows placing the piece covering places 3, 4, 8, and C. That is, the piece may wrap around the board. To prohibit this, we add a new dummy-column to the board, so that it looks like
0123G 4567H 89ABI CDEFJ
The variables for places G to J are all set to zero initially, and the regular expression for the placement of the piece is modified to include the extra column, 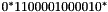 .
.
Rotating pieces
To handle rotations of the piece, we can use disjunctions of regular expressions for all the relevant rotations. Consider the rotated version of the above piece, depicted below.
X XXX
The corresponding regular expression for this piece is 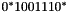 . To combine these two regular expressions, we can simply use disjunction of regular expressions, arriving at the expression
. To combine these two regular expressions, we can simply use disjunction of regular expressions, arriving at the expression 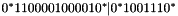 for enforcing the placement of the piece in one of the above two rotations.
for enforcing the placement of the piece in one of the above two rotations.
There are 8 symmetries for the pieces in general. The 8 disjuncts for a particular piece might, however, contain less than 8 distinct expressions (for example, any square has only one distinct disjunct). This is removed when then automaton for the expression is computed, since it is minimized.
Placing several pieces
To generalize the above model to several pieces, we let the variables range from 0 to n, where n is the number of pieces to place. Given that we place three pieces, and that the above shown piece is number one, we will replace each 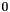 -expression with the expression
-expression with the expression 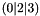 . Thus, the second regular expression becomes
. Thus, the second regular expression becomes 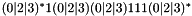 . Additionaly, the end of line marker gets its own value.
. Additionaly, the end of line marker gets its own value.
This generalization suffers from the fact that the automata become much more complex. This problem can be solved by instead projecting out each component, which gives a new board of 0/1-variables for each piece to place.
The Branching
This model does not use any advanced heuristic for the branching. The variables selection is simply in order, and the value selection is minimum value first.
The static value selection allows us to order the pieces in the specification of the problem. The pieces are approximately ordered by largness or hardness to place.
Removing board symmetries
Especially when searching for all solutions of a puzzle instance, we might want to remove the symmetrical boards from the solutions-space. This is done using the same symmetry functions as for the piece symmetries and lexicographical order constraints.
Definition at line 261 of file pentominoes.cpp.
Member Enumeration Documentation
| anonymous enum |
Choice of propagators.
Definition at line 264 of file pentominoes.cpp.
| anonymous enum |
Choice of symmetry breaking.
- Enumerator:
SYMMETRY_NONE Do not remove symmetric solutions.
SYMMETRY_FULL Remove symmetric solutions.
Definition at line 269 of file pentominoes.cpp.
Constructor & Destructor Documentation
| Pentominoes::Pentominoes | ( | const SizeOptions & | opt | ) | [inline] |
Construction of the model.
Definition at line 337 of file pentominoes.cpp.
| Pentominoes::Pentominoes | ( | Pentominoes & | s | ) | [inline] |
Constructor for cloning s.
Definition at line 439 of file pentominoes.cpp.
Member Function Documentation
| virtual Space* Pentominoes::copy | ( | void | ) | [inline, virtual] |
Copy space during cloning.
Definition at line 447 of file pentominoes.cpp.
| virtual void Pentominoes::print | ( | std::ostream & | os | ) | const [inline, virtual] |
Print solution.
Reimplemented from Gecode::Driver::ScriptBase< BaseSpace >.
Definition at line 453 of file pentominoes.cpp.
Friends And Related Function Documentation
typedef void(* tsymmfunc)(const char *, int, int, char *, int &, int &) [related] |
Type for tile symmetry functions.
Definition at line 95 of file pentominoes.cpp.
typedef void(* bsymmfunc)(const IntVarArgs, int, int, IntVarArgs &, int &, int &) [related] |
Type for board symmetry functions.
Definition at line 97 of file pentominoes.cpp.
Board specifications.
List of specifications.
Each board specification repurposes the first two TileSpecs to record width and height of the board (TileSpec 0) as well as the number of tiles and whether the board is filled (TileSpec 1).
Definition at line 68 of file pentominoes.cpp.
const int examples_size[] [related] |
{sizeof(puzzle0)/sizeof(TileSpec),
sizeof(puzzle1)/sizeof(TileSpec),
sizeof(square2)/sizeof(TileSpec),
sizeof(square3)/sizeof(TileSpec),
sizeof(pentomino6x10)/sizeof(TileSpec),
sizeof(pentomino5x12)/sizeof(TileSpec),
sizeof(pentomino4x15)/sizeof(TileSpec),
sizeof(pentomino3x20)/sizeof(TileSpec)}
Board specification sizes.
Definition at line 73 of file pentominoes.cpp.
const unsigned int n_examples [related] |
Number of board specifications.
Definition at line 78 of file pentominoes.cpp.
{
{4, 4, true, ""},
{2, 3, 1,
"XX"
"X "
"X "},
{2, 1, 1,
"XX"},
{3, 3, 1,
" XX"
" X"
"XXX"},
{1, 1, 1,
"X"},
{3, 1, 1,
"XXX"}
}
Small specification.
Definition at line 504 of file pentominoes.cpp.
Standard specification.
Definition at line 524 of file pentominoes.cpp.
{
{10, 10, true, ""},
{6, 6, 1,
"XXXXXX"
"XXXXXX"
"XXXXXX"
"XXXXXX"
"XXXXXX"
"XXXXXX"
},
{4, 4, 3,
"XXXX"
"XXXX"
"XXXX"
"XXXX"},
{2, 2, 4,
"XX"
"XX"}
}
Board specifications.
List of specifications.
Each board specification repurposes the first two TileSpecs to record width and height of the board (TileSpec 0) as well as the number of tiles and whether the board is filled (TileSpec 1).
Definition at line 574 of file pentominoes.cpp.
Board specifications.
List of specifications.
Each board specification repurposes the first two TileSpecs to record width and height of the board (TileSpec 0) as well as the number of tiles and whether the board is filled (TileSpec 1).
Definition at line 597 of file pentominoes.cpp.
const TileSpec pentomino6x10[] [related] |
Board specifications.
List of specifications.
Each board specification repurposes the first two TileSpecs to record width and height of the board (TileSpec 0) as well as the number of tiles and whether the board is filled (TileSpec 1).
Definition at line 654 of file pentominoes.cpp.
const TileSpec pentomino5x12[] [related] |
Board specifications.
List of specifications.
Each board specification repurposes the first two TileSpecs to record width and height of the board (TileSpec 0) as well as the number of tiles and whether the board is filled (TileSpec 1).
Definition at line 706 of file pentominoes.cpp.
const TileSpec pentomino4x15[] [related] |
Board specifications.
List of specifications.
Each board specification repurposes the first two TileSpecs to record width and height of the board (TileSpec 0) as well as the number of tiles and whether the board is filled (TileSpec 1).
Definition at line 758 of file pentominoes.cpp.
const TileSpec pentomino3x20[] [related] |
Board specifications.
List of specifications.
Each board specification repurposes the first two TileSpecs to record width and height of the board (TileSpec 0) as well as the number of tiles and whether the board is filled (TileSpec 1).
Definition at line 810 of file pentominoes.cpp.
const unsigned n_examples = sizeof(examples)/sizeof(TileSpec*) [related] |
Number of specifications.
Definition at line 876 of file pentominoes.cpp.
| int pos | ( | int | h, | |
| int | w, | |||
| int | h1, | |||
| int | w1 | |||
| ) | [related] |
Return index of (h, w) in the row-major layout of a matrix with width w1 and height h1.
| void id | ( | CArray | t1, | |
| int | w1, | |||
| int | h1, | |||
| Array | t2, | |||
| int & | w2, | |||
| int & | h2 | |||
| ) | [related] |
Identity symmetry.
| void rot90 | ( | CArray | t1, | |
| int | w1, | |||
| int | h1, | |||
| Array | t2, | |||
| int & | w2, | |||
| int & | h2 | |||
| ) | [related] |
Rotate 90 degrees.
| void rot180 | ( | CArray | t1, | |
| int | w1, | |||
| int | h1, | |||
| Array | t2, | |||
| int & | w2, | |||
| int & | h2 | |||
| ) | [related] |
Rotate 180 degrees.
| void rot270 | ( | CArray | t1, | |
| int | w1, | |||
| int | h1, | |||
| Array | t2, | |||
| int & | w2, | |||
| int & | h2 | |||
| ) | [related] |
Rotate 270 degrees.
| void flipx | ( | CArray | t1, | |
| int | w1, | |||
| int | h1, | |||
| Array | t2, | |||
| int & | w2, | |||
| int & | h2 | |||
| ) | [related] |
Flip x-wise.
| void flipy | ( | CArray | t1, | |
| int | w1, | |||
| int | h1, | |||
| Array | t2, | |||
| int & | w2, | |||
| int & | h2 | |||
| ) | [related] |
Flip y-wise.
| void flipd1 | ( | CArray | t1, | |
| int | w1, | |||
| int | h1, | |||
| Array | t2, | |||
| int & | w2, | |||
| int & | h2 | |||
| ) | [related] |
Flip diagonal 1.
| void flipd2 | ( | CArray | t1, | |
| int | w1, | |||
| int | h1, | |||
| Array | t2, | |||
| int & | w2, | |||
| int & | h2 | |||
| ) | [related] |
Flip diagonal 2.
List of specifications.
Definition at line 863 of file pentominoes.cpp.
| const int examples_size | ( | ) | [related] |
Board specifications.
List of specifications.
Each board specification repurposes the first two TileSpecs to record width and height of the board (TileSpec 0) as well as the number of tiles and whether the board is filled (TileSpec 1).
Definition at line 866 of file pentominoes.cpp.
The documentation for this class was generated from the following file:
- examples/pentominoes.cpp
