Linear constraints over integer variables
[Using integer variables and constraints]
Functions | |
| void | Gecode::linear (Home home, const IntVarArgs &x, IntRelType irt, int c, IntPropLevel ipl=IPL_DEF) |
Post propagator for 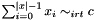 . . | |
| void | Gecode::linear (Home home, const IntVarArgs &x, IntRelType irt, IntVar y, IntPropLevel ipl=IPL_DEF) |
Post propagator for 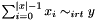 . . | |
| void | Gecode::linear (Home home, const IntVarArgs &x, IntRelType irt, int c, Reify r, IntPropLevel ipl=IPL_DEF) |
Post propagator for 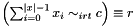 . . | |
| void | Gecode::linear (Home home, const IntVarArgs &x, IntRelType irt, IntVar y, Reify r, IntPropLevel ipl=IPL_DEF) |
Post propagator for 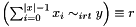 . . | |
| void | Gecode::linear (Home home, const IntArgs &a, const IntVarArgs &x, IntRelType irt, int c, IntPropLevel ipl=IPL_DEF) |
Post propagator for 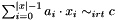 . . | |
| void | Gecode::linear (Home home, const IntArgs &a, const IntVarArgs &x, IntRelType irt, IntVar y, IntPropLevel ipl=IPL_DEF) |
Post propagator for 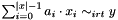 . . | |
| void | Gecode::linear (Home home, const IntArgs &a, const IntVarArgs &x, IntRelType irt, int c, Reify r, IntPropLevel ipl=IPL_DEF) |
Post propagator for 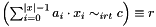 . . | |
| void | Gecode::linear (Home home, const IntArgs &a, const IntVarArgs &x, IntRelType irt, IntVar y, Reify r, IntPropLevel ipl=IPL_DEF) |
Post propagator for 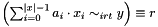 . . | |
Detailed Description
All variants for linear constraints over integer variables share the following properties:
- Bounds consistency (over the real numbers) is supported for all constraints (actually, for disequlities always domain consistency is used as it is cheaper). Domain consistency is supported for all non-reified constraint. As bounds consistency for inequalities coincides with domain consistency, the only real variation is for linear equations. Domain consistent linear equations have exponential complexity, so use with care!
- If the integer propagation level IPL_DEF is used as argument (hence, default propagation) and the linear constraint is sufficiently simple (two variables with unit coefficients), the domain consistent propagation is used.
- Variables occurring multiply in the argument arrays are replaced by a single occurrence: for example,
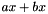 becomes
becomes 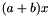 .
. - If in the above simplification the value for
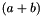 (or for
(or for 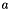 and
and 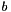 ) exceeds the limits for integers as defined in Int::Limits, an exception of type Int::OutOfLimits is thrown.
) exceeds the limits for integers as defined in Int::Limits, an exception of type Int::OutOfLimits is thrown. - Assume the constraint
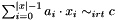 . If
. If 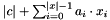 exceeds the maximal available precision (at least
exceeds the maximal available precision (at least 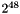 ), an exception of type Int::OutOfLimits is thrown.
), an exception of type Int::OutOfLimits is thrown. - In all other cases, the created propagators are accurate (that is, they will not silently overflow during propagation).
Function Documentation
| void Gecode::linear | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| int | c, | |||
| IntPropLevel | ipl | |||
| ) |
Post propagator for 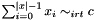 .
.
| void Gecode::linear | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| IntVar | y, | |||
| IntPropLevel | ipl | |||
| ) |
Post propagator for 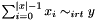 .
.
| void Gecode::linear | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| int | c, | |||
| Reify | r, | |||
| IntPropLevel | ||||
| ) |
Post propagator for 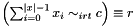 .
.
| void Gecode::linear | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| IntVar | y, | |||
| Reify | r, | |||
| IntPropLevel | ||||
| ) |
Post propagator for 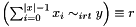 .
.
| void Gecode::linear | ( | Home | home, | |
| const IntArgs & | a, | |||
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| int | c, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 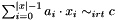 .
.
Throws an exception of type Int::ArgumentSizeMismatch, if a and x are of different size.
| void Gecode::linear | ( | Home | home, | |
| const IntArgs & | a, | |||
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| IntVar | y, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 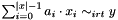 .
.
Throws an exception of type Int::ArgumentSizeMismatch, if a and x are of different size.
| void Gecode::linear | ( | Home | home, | |
| const IntArgs & | a, | |||
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| int | c, | |||
| Reify | r, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 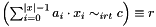 .
.
Throws an exception of type Int::ArgumentSizeMismatch, if a and x are of different size.
| void Gecode::linear | ( | Home | home, | |
| const IntArgs & | a, | |||
| const IntVarArgs & | x, | |||
| IntRelType | irt, | |||
| IntVar | y, | |||
| Reify | r, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 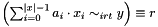 .
.
Throws an exception of type Int::ArgumentSizeMismatch, if a and x are of different size.
