Graph constraints
[Using integer variables and constraints]
Functions | |
| void | Gecode::circuit (Home home, const IntVarArgs &x, IntPropLevel ipl=IPL_DEF) |
| Post propagator such that x forms a circuit. | |
| void | Gecode::circuit (Home home, int offset, const IntVarArgs &x, IntPropLevel ipl=IPL_DEF) |
| Post propagator such that x forms a circuit. | |
| void | Gecode::circuit (Home home, const IntArgs &c, const IntVarArgs &x, const IntVarArgs &y, IntVar z, IntPropLevel ipl=IPL_DEF) |
| Post propagator such that x forms a circuit with costs y and z. | |
| void | Gecode::circuit (Home home, const IntArgs &c, int offset, const IntVarArgs &x, const IntVarArgs &y, IntVar z, IntPropLevel ipl=IPL_DEF) |
| Post propagator such that x forms a circuit with costs y and z. | |
| void | Gecode::circuit (Home home, const IntArgs &c, const IntVarArgs &x, IntVar z, IntPropLevel ipl=IPL_DEF) |
| Post propagator such that x forms a circuit with cost z. | |
| void | Gecode::circuit (Home home, const IntArgs &c, int offset, const IntVarArgs &x, IntVar z, IntPropLevel ipl=IPL_DEF) |
| Post propagator such that x forms a circuit with cost z. | |
| void | Gecode::path (Home home, const IntVarArgs &x, IntVar s, IntVar e, IntPropLevel ipl=IPL_DEF) |
| Post propagator such that x forms a Hamiltonian path. | |
| void | Gecode::path (Home home, int offset, const IntVarArgs &x, IntVar s, IntVar e, IntPropLevel ipl=IPL_DEF) |
| Post propagator such that x forms a Hamiltonian path. | |
| void | Gecode::path (Home home, const IntArgs &c, const IntVarArgs &x, IntVar s, IntVar e, const IntVarArgs &y, IntVar z, IntPropLevel ipl=IPL_DEF) |
| Post propagator such that x forms a Hamiltonian path with costs y and z. | |
| void | Gecode::path (Home home, const IntArgs &c, int offset, const IntVarArgs &x, IntVar s, IntVar e, const IntVarArgs &y, IntVar z, IntPropLevel ipl=IPL_DEF) |
| Post propagator such that x forms a Hamiltonian path with costs y and z. | |
| void | Gecode::path (Home home, const IntArgs &c, const IntVarArgs &x, IntVar s, IntVar e, IntVar z, IntPropLevel ipl=IPL_DEF) |
| Post propagator such that x forms a Hamiltonian path with cost z. | |
| void | Gecode::path (Home home, const IntArgs &c, int offset, const IntVarArgs &x, IntVar s, IntVar e, IntVar z, IntPropLevel ipl=IPL_DEF) |
| Post propagator such that x forms a Hamiltonian path with cost z. | |
Function Documentation
| void Gecode::circuit | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator such that x forms a circuit.
x forms a circuit if the graph with edges 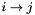 where
where 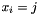 has a single cycle covering all nodes.
has a single cycle covering all nodes.
Supports domain (ipl = IPL_DOM) and value propagation (all other values for ipl), where this refers to whether value or domain consistent distinct in enforced on x.
Throws the following exceptions:
- Int::ArgumentSame, if x contains the same unassigned variable multiply.
- Int::TooFewArguments, if x has no elements.
| void Gecode::circuit | ( | Home | home, | |
| int | offset, | |||
| const IntVarArgs & | x, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator such that x forms a circuit.
x forms a circuit if the graph with edges 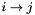 where
where  has a single cycle covering all nodes.
has a single cycle covering all nodes.
Supports domain (ipl = IPL_DOM) and value propagation (all other values for ipl), where this refers to whether value or domain consistent distinct in enforced on x.
Throws the following exceptions:
- Int::ArgumentSame, if x contains the same unassigned variable multiply.
- Int::TooFewArguments, if x has no elements.
- Int::OutOfLimits, if offset is negative.
| void Gecode::circuit | ( | Home | home, | |
| const IntArgs & | c, | |||
| const IntVarArgs & | x, | |||
| const IntVarArgs & | y, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator such that x forms a circuit with costs y and z.
x forms a circuit if the graph with edges 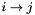 where
where 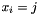 has a single cycle covering all nodes. The integer array c gives the costs of all possible edges where
has a single cycle covering all nodes. The integer array c gives the costs of all possible edges where 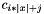 is the cost of the edge
is the cost of the edge 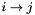 . The variable z is the cost of the entire circuit. The variables y define the cost of the edge in x: that is, if
. The variable z is the cost of the entire circuit. The variables y define the cost of the edge in x: that is, if 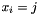 then
then 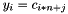 .
.
Supports domain (ipl = IPL_DOM) and value propagation (all other values for ipl), where this refers to whether value or domain consistent distinct in enforced on x for circuit.
Throws the following exceptions:
- Int::ArgumentSame, if x contains the same unassigned variable multiply.
- Int::TooFewArguments, if x has no elements.
- Int::ArgumentSizeMismatch, if x and y do not have the same size or if
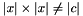 .
.
| void Gecode::circuit | ( | Home | home, | |
| const IntArgs & | c, | |||
| int | offset, | |||
| const IntVarArgs & | x, | |||
| const IntVarArgs & | y, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator such that x forms a circuit with costs y and z.
x forms a circuit if the graph with edges 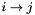 where
where  has a single cycle covering all nodes. The integer array c gives the costs of all possible edges where
has a single cycle covering all nodes. The integer array c gives the costs of all possible edges where 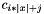 is the cost of the edge
is the cost of the edge 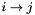 . The variable z is the cost of the entire circuit. The variables y define the cost of the edge in x: that is, if
. The variable z is the cost of the entire circuit. The variables y define the cost of the edge in x: that is, if 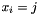 then
then 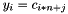 .
.
Supports domain (ipl = IPL_DOM) and value propagation (all other values for ipl), where this refers to whether value or domain consistent distinct in enforced on x for circuit.
Throws the following exceptions:
- Int::ArgumentSame, if x contains the same unassigned variable multiply.
- Int::TooFewArguments, if x has no elements.
- Int::ArgumentSizeMismatch, if x and y do not have the same size or if
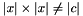 .
. - Int::OutOfLimits, if offset is negative.
| void Gecode::circuit | ( | Home | home, | |
| const IntArgs & | c, | |||
| const IntVarArgs & | x, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator such that x forms a circuit with cost z.
x forms a circuit if the graph with edges 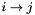 where
where 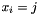 has a single cycle covering all nodes. The integer array c gives the costs of all possible edges where
has a single cycle covering all nodes. The integer array c gives the costs of all possible edges where 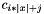 is the cost of the edge
is the cost of the edge 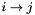 . The variable z is the cost of the entire circuit.
. The variable z is the cost of the entire circuit.
Supports domain (ipl = IPL_DOM) and value propagation (all other values for ipl), where this refers to whether value or domain consistent distinct in enforced on x for circuit.
Throws the following exceptions:
- Int::ArgumentSame, if x contains the same unassigned variable multiply.
- Int::TooFewArguments, if x has no elements.
- Int::ArgumentSizeMismatch, if
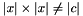 .
.
| void Gecode::circuit | ( | Home | home, | |
| const IntArgs & | c, | |||
| int | offset, | |||
| const IntVarArgs & | x, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator such that x forms a circuit with cost z.
x forms a circuit if the graph with edges 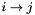 where
where  has a single cycle covering all nodes. The integer array c gives the costs of all possible edges where
has a single cycle covering all nodes. The integer array c gives the costs of all possible edges where 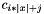 is the cost of the edge
is the cost of the edge 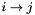 . The variable z is the cost of the entire circuit.
. The variable z is the cost of the entire circuit.
Supports domain (ipl = IPL_DOM) and value propagation (all other values for ipl), where this refers to whether value or domain consistent distinct in enforced on x for circuit.
Throws the following exceptions:
- Int::ArgumentSame, if x contains the same unassigned variable multiply.
- Int::TooFewArguments, if x has no elements.
- Int::ArgumentSizeMismatch, if
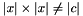 .
. - Int::OutOfLimits, if offset is negative.
| void Gecode::path | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntVar | s, | |||
| IntVar | e, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator such that x forms a Hamiltonian path.
x forms a Hamiltonian path if the graph with edges 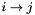 where
where 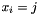 visits all nodes exactly once. The path starts at node s and the successor of the last node e is equal to
visits all nodes exactly once. The path starts at node s and the successor of the last node e is equal to 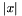 .
.
Supports domain (ipl = IPL_DOM) and value propagation (all other values for ipl), where this refers to whether value or domain consistent distinct in enforced on x.
Throws the following exceptions:
- Int::ArgumentSame, if x contains the same unassigned variable multiply.
- Int::TooFewArguments, if x has no elements.
| void Gecode::path | ( | Home | home, | |
| int | offset, | |||
| const IntVarArgs & | x, | |||
| IntVar | s, | |||
| IntVar | e, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator such that x forms a Hamiltonian path.
x forms a Hamiltonian path if the graph with edges 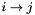 where
where  visits all nodes exactly once. The path starts at node s and the successor of the last node e is equal to
visits all nodes exactly once. The path starts at node s and the successor of the last node e is equal to 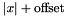 .
.
Supports domain (ipl = IPL_DOM) and value propagation (all other values for ipl), where this refers to whether value or domain consistent distinct in enforced on x.
Throws the following exceptions:
- Int::ArgumentSame, if x contains the same unassigned variable multiply.
- Int::TooFewArguments, if x has no elements.
- Int::OutOfLimits, if offset is negative.
| void Gecode::path | ( | Home | home, | |
| const IntArgs & | c, | |||
| const IntVarArgs & | x, | |||
| IntVar | s, | |||
| IntVar | e, | |||
| const IntVarArgs & | y, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator such that x forms a Hamiltonian path with costs y and z.
x forms a Hamiltonian path if the graph with edges 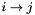 where
where 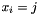 visits all nodes exactly once. The path starts at node s and the successor of the last node e is equal to
visits all nodes exactly once. The path starts at node s and the successor of the last node e is equal to 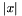 . The integer array c gives the costs of all possible edges where
. The integer array c gives the costs of all possible edges where 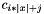 is the cost of the edge
is the cost of the edge 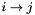 . The variable z is the cost of the entire path. The variables y define the cost of the edge in x: that is, if
. The variable z is the cost of the entire path. The variables y define the cost of the edge in x: that is, if 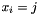 then
then 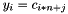 .
.
Supports domain (ipl = IPL_DOM) and value propagation (all other values for ipl), where this refers to whether value or domain consistent distinct in enforced on x for circuit.
Throws the following exceptions:
- Int::ArgumentSame, if x contains the same unassigned variable multiply.
- Int::TooFewArguments, if x has no elements.
- Int::ArgumentSizeMismacth, if x and y do not have the same size or if
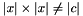 .
.
| void Gecode::path | ( | Home | home, | |
| const IntArgs & | c, | |||
| int | offset, | |||
| const IntVarArgs & | x, | |||
| IntVar | s, | |||
| IntVar | e, | |||
| const IntVarArgs & | y, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator such that x forms a Hamiltonian path with costs y and z.
x forms a Hamiltonian path if the graph with edges 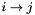 where
where  visits all nodes exactly once. The path starts at node s and the successor of the last node e is equal to
visits all nodes exactly once. The path starts at node s and the successor of the last node e is equal to 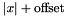 . The integer array c gives the costs of all possible edges where
. The integer array c gives the costs of all possible edges where 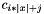 is the cost of the edge
is the cost of the edge 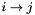 . The variable z is the cost of the entire path. The variables y define the cost of the edge in x: that is, if
. The variable z is the cost of the entire path. The variables y define the cost of the edge in x: that is, if 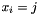 then
then 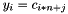 .
.
Supports domain (ipl = IPL_DOM) and value propagation (all other values for ipl), where this refers to whether value or domain consistent distinct in enforced on x for circuit.
Throws the following exceptions:
- Int::ArgumentSame, if x contains the same unassigned variable multiply.
- Int::TooFewArguments, if x has no elements.
- Int::ArgumentSizeMismacth, if x and y do not have the same size or if
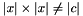 .
. - Int::OutOfLimits, if offset is negative.
| void Gecode::path | ( | Home | home, | |
| const IntArgs & | c, | |||
| const IntVarArgs & | x, | |||
| IntVar | s, | |||
| IntVar | e, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator such that x forms a Hamiltonian path with cost z.
x forms a Hamiltonian path if the graph with edges 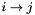 where
where 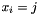 visits all nodes exactly once. The path starts at node s and the successor of the last node e is equal to
visits all nodes exactly once. The path starts at node s and the successor of the last node e is equal to 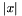 . The integer array c gives the costs of all possible edges where
. The integer array c gives the costs of all possible edges where 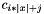 is the cost of the edge
is the cost of the edge 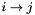 . The variable z is the cost of the entire path.
. The variable z is the cost of the entire path.
Supports domain (ipl = IPL_DOM) and value propagation (all other values for ipl), where this refers to whether value or domain consistent distinct in enforced on x for circuit.
Throws the following exceptions:
- Int::ArgumentSame, if x contains the same unassigned variable multiply.
- Int::TooFewArguments, if x has no elements.
- Int::ArgumentSizeMismacth, if
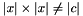 .
.
| void Gecode::path | ( | Home | home, | |
| const IntArgs & | c, | |||
| int | offset, | |||
| const IntVarArgs & | x, | |||
| IntVar | s, | |||
| IntVar | e, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator such that x forms a Hamiltonian path with cost z.
x forms a Hamiltonian path if the graph with edges 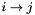 where
where  visits all nodes exactly once. The path starts at node s and the successor of the last node e is equal to
visits all nodes exactly once. The path starts at node s and the successor of the last node e is equal to 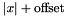 . The integer array c gives the costs of all possible edges where
. The integer array c gives the costs of all possible edges where 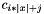 is the cost of the edge
is the cost of the edge 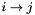 . The variable z is the cost of the entire circuit.
. The variable z is the cost of the entire circuit.
Supports domain (ipl = IPL_DOM) and value propagation (all other values for ipl), where this refers to whether value or domain consistent distinct in enforced on x for circuit.
Throws the following exceptions:
- Int::ArgumentSame, if x contains the same unassigned variable multiply.
- Int::TooFewArguments, if x has no elements.
- Int::ArgumentSizeMismacth, if
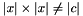 .
. - Int::OutOfLimits, if offset is negative.
