Counting constraints
[Using integer variables and constraints]
Functions | |
| void | Gecode::count (Home home, const IntVarArgs &x, int n, IntRelType irt, int m, IntPropLevel ipl=IPL_DEF) |
Post propagator for 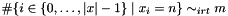 . . | |
| void | Gecode::count (Home home, const IntVarArgs &x, const IntSet &y, IntRelType irt, int m, IntPropLevel ipl=IPL_DEF) |
Post propagator for 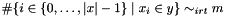 . . | |
| void | Gecode::count (Home home, const IntVarArgs &x, IntVar y, IntRelType irt, int m, IntPropLevel ipl=IPL_DEF) |
Post propagator for 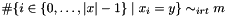 . . | |
| void | Gecode::count (Home home, const IntVarArgs &x, const IntArgs &y, IntRelType irt, int m, IntPropLevel ipl=IPL_DEF) |
Post propagator for 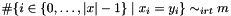 . . | |
| void | Gecode::count (Home home, const IntVarArgs &x, int n, IntRelType irt, IntVar z, IntPropLevel ipl=IPL_DEF) |
Post propagator for 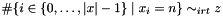 . . | |
| void | Gecode::count (Home home, const IntVarArgs &x, const IntSet &y, IntRelType irt, IntVar z, IntPropLevel ipl=IPL_DEF) |
Post propagator for 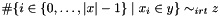 . . | |
| void | Gecode::count (Home home, const IntVarArgs &x, IntVar y, IntRelType irt, IntVar z, IntPropLevel ipl=IPL_DEF) |
Post propagator for 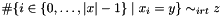 . . | |
| void | Gecode::count (Home home, const IntVarArgs &x, const IntArgs &y, IntRelType irt, IntVar z, IntPropLevel ipl=IPL_DEF) |
Post propagator for 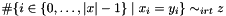 . . | |
| void | Gecode::count (Home home, const IntVarArgs &x, const IntVarArgs &c, IntPropLevel ipl=IPL_DEF) |
| Posts a global count (cardinality) constraint. | |
| void | Gecode::count (Home home, const IntVarArgs &x, const IntSetArgs &c, IntPropLevel ipl=IPL_DEF) |
| Posts a global count (cardinality) constraint. | |
| void | Gecode::count (Home home, const IntVarArgs &x, const IntVarArgs &c, const IntArgs &v, IntPropLevel ipl=IPL_DEF) |
| Posts a global count (cardinality) constraint. | |
| void | Gecode::count (Home home, const IntVarArgs &x, const IntSetArgs &c, const IntArgs &v, IntPropLevel ipl=IPL_DEF) |
| Posts a global count (cardinality) constraint. | |
| void | Gecode::count (Home home, const IntVarArgs &x, const IntSet &c, const IntArgs &v, IntPropLevel ipl=IPL_DEF) |
| Posts a global count (cardinality) constraint. | |
Detailed Description
- Note:
- Domain consistency on the extended cardinality variables of the Global Cardinality Propagator is only obtained if they are bounds consistent, otherwise the problem of enforcing domain consistency on the cardinality variables is NP-complete as proved by Qumiper et. al. in ''Improved Algorithms for the Global Cardinality Constraint''.
Function Documentation
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| int | n, | |||
| IntRelType | irt, | |||
| int | m, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 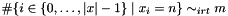 .
.
Performs domain propagation but is not domain consistent.
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| const IntSet & | y, | |||
| IntRelType | irt, | |||
| int | m, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 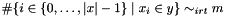 .
.
Performs domain propagation but is not domain consistent.
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntVar | y, | |||
| IntRelType | irt, | |||
| int | m, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 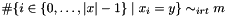 .
.
Performs domain propagation (ipl = IPL_DOM, default) and slightly less domain propagation (all other values for ipl), where y is not pruned. Note that in both cases propagation is not domain consistent.
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| const IntArgs & | y, | |||
| IntRelType | irt, | |||
| int | m, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 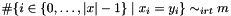 .
.
Performs domain propagation but is not domain consistent.
Throws an exception of type Int::ArgumentSizeMismatch, if x and y are of different size.
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| int | n, | |||
| IntRelType | irt, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 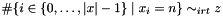 .
.
Performs domain propagation but is not domain consistent.
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| const IntSet & | y, | |||
| IntRelType | irt, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 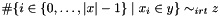 .
.
Performs domain propagation but is not domain consistent.
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| IntVar | y, | |||
| IntRelType | irt, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 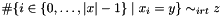 .
.
Performs domain propagation (ipl = IPL_DOM, default) and slightly less domain propagation (all other values for ipl), where y is not pruned. Note that in both cases propagation is not domain consistent.
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| const IntArgs & | y, | |||
| IntRelType | irt, | |||
| IntVar | z, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Post propagator for 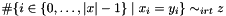 .
.
Performs domain propagation but is not domain consistent.
Throws an exception of type Int::ArgumentSizeMismatch, if x and y are of different size.
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| const IntVarArgs & | c, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Posts a global count (cardinality) constraint.
Posts the constraint that 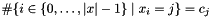 and
and 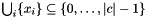 (no other value occurs).
(no other value occurs).
Supports value (ipl = IPL_VAL, default), bounds (ipl = IPL_BND), and domain consistency (ipl = IPL_DOM).
Throws an exception of type Int::ArgumentSame, if x contains the same unassigned variable multiply.
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| const IntSetArgs & | c, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Posts a global count (cardinality) constraint.
Posts the constraint that 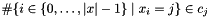 and
and 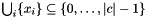 (no other value occurs).
(no other value occurs).
Supports value (ipl = IPL_VAL, default), bounds (ipl = IPL_BND), and domain consistency (ipl = IPL_DOM).
Throws an exception of type Int::ArgumentSame, if x contains the same unassigned variable multiply.
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| const IntVarArgs & | c, | |||
| const IntArgs & | v, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Posts a global count (cardinality) constraint.
Posts the constraint that 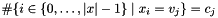 and
and 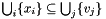 (no other value occurs).
(no other value occurs).
Supports value (ipl = IPL_VAL, default), bounds (ipl = IPL_BND), and domain consistency (ipl = IPL_DOM).
Throws an exception of type Int::ArgumentSame, if x contains the same unassigned variable multiply.
Throws an exception of type Int::ArgumentSizeMismatch, if c and v are of different size.
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| const IntSetArgs & | c, | |||
| const IntArgs & | v, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Posts a global count (cardinality) constraint.
Posts the constraint that 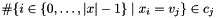 and
and 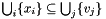 (no other value occurs).
(no other value occurs).
Supports value (ipl = IPL_VAL, default), bounds (ipl = IPL_BND), and domain consistency (ipl = IPL_DOM).
Throws an exception of type Int::ArgumentSame, if x contains the same unassigned variable multiply.
Throws an exception of type Int::ArgumentSizeMismatch, if c and v are of different size.
| void Gecode::count | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| const IntSet & | c, | |||
| const IntArgs & | v, | |||
| IntPropLevel | ipl = IPL_DEF | |||
| ) |
Posts a global count (cardinality) constraint.
Posts the constraint that 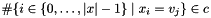 and
and 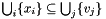 (no other value occurs).
(no other value occurs).
Supports value (ipl = IPL_VAL, default), bounds (ipl = IPL_BND), and domain consistency (ipl = IPL_DOM).
Throws an exception of type Int::ArgumentSame, if x contains the same unassigned variable multiply.
Throws an exception of type Int::ArgumentSizeMismatch, if c and v are of different size.
