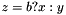Simple relation constraints over float variables
[Using float variables and constraints]

Functions
void	Gecode::rel (Home home, FloatVar x0, FloatRelType frt, FloatVar x1)
	Post propagator for 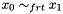$x_0 \sim_{frt} x_1$ .
void	Gecode::rel (Home home, FloatVar x, FloatRelType frt, FloatVal c)
	Propagates 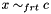$x \sim_{frt} c$ .
void	Gecode::rel (Home home, FloatVar x, FloatRelType frt, FloatVal c, Reify r)
	Post propagator for 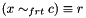$(x \sim_{frt} c)\equiv r$ .
void	Gecode::rel (Home home, FloatVar x0, FloatRelType frt, FloatVar x1, Reify r)
	Post propagator for 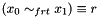$(x_0 \sim_{frt} x_1)\equiv r$ .
void	Gecode::rel (Home home, const FloatVarArgs &x, FloatRelType frt, FloatVal c)
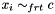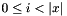	Propagates $x_i \sim_{frt} c$ for all $0\leq i<\|x\|$ .
void	Gecode::rel (Home home, const FloatVarArgs &x, FloatRelType frt, FloatVar y)
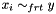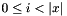	Propagates $x_i \sim_{frt} y$ for all $0\leq i<\|x\|$ .
void	Gecode::ite (Home home, BoolVar b, FloatVar x, FloatVar y, FloatVar z)
	Post propagator for if-then-else constraint.

Function Documentation

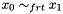Post propagator for $x_0 \sim_{frt} x_1$ .

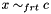Propagates $x \sim_{frt} c$ .

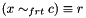Post propagator for $(x \sim_{frt} c)\equiv r$ .

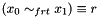Post propagator for $(x_0 \sim_{frt} x_1)\equiv r$ .

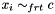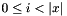Propagates $x_i \sim_{frt} c$ for all $0\leq i<|x|$ .

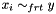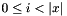Propagates $x_i \sim_{frt} y$ for all $0\leq i<|x|$ .

Post propagator for if-then-else constraint.

Posts propagator for $ z = b ? x : y $