Element constraints
[Using finite integer sets]
Functions | |
| void | Gecode::element (Home home, SetOpType op, const SetVarArgs &x, SetVar y, SetVar z, const IntSet &u=IntSet(Set::Limits::min, Set::Limits::max)) |
Post propagator for ![$ z=\diamond_{\mathit{op}}\langle x_0,\dots,x_{n-1}\rangle[y] $](form_415.png) . . | |
| void | Gecode::element (Home home, SetOpType op, const IntVarArgs &x, SetVar y, SetVar z, const IntSet &u=IntSet(Set::Limits::min, Set::Limits::max)) |
Post propagator for ![$ z=\diamond_{\mathit{op}}\langle \{x_0\},\dots,\{x_{n-1}\}\rangle[y] $](form_416.png) . . | |
| void | Gecode::element (Home home, SetOpType op, const IntSetArgs &x, SetVar y, SetVar z, const IntSet &u=IntSet(Set::Limits::min, Set::Limits::max)) |
Post propagator for ![$ z=\diamond_{\mathit{op}}\langle x_0,\dots,x_{n-1}\rangle[y] $](form_415.png) . . | |
| void | Gecode::element (Home home, SetOpType op, const IntArgs &x, SetVar y, SetVar z, const IntSet &u=IntSet(Set::Limits::min, Set::Limits::max)) |
Post propagator for ![$ z=\diamond_{\mathit{op}}\langle \{x_0\},\dots,\{x_{n-1}\}\rangle[y] $](form_416.png) . . | |
| void | Gecode::element (Home home, const SetVarArgs &x, IntVar y, SetVar z) |
Post propagator for ![$ z=\langle x_0,\dots,x_{n-1}\rangle[y] $](form_417.png) . . | |
| void | Gecode::element (Home home, const IntSetArgs &s, IntVar y, SetVar z) |
Post propagator for ![$ z=\langle s_0,\dots,s_{n-1}\rangle[y] $](form_418.png) . . | |
| void | Gecode::element (Home home, const IntSetArgs &a, IntVar x, int w, IntVar y, int h, SetVar z) |
Post propagator for 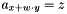 . . | |
| void | Gecode::element (Home home, const SetVarArgs &a, IntVar x, int w, IntVar y, int h, SetVar z) |
Post propagator for 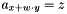 . . | |
Detailed Description
An element constraint selects zero, one or more elements out of a sequence. We write 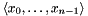 for the sequence, and
for the sequence, and ![$ [y] $](form_414.png) for the index variable.
for the index variable.
Set element constraints are closely related to the element constraint on integer variables.
Function Documentation
| void Gecode::element | ( | Home | home, | |
| SetOpType | op, | |||
| const SetVarArgs & | x, | |||
| SetVar | y, | |||
| SetVar | z, | |||
| const IntSet & | u = IntSet(Set::Limits::min, Set::Limits::max) | |||
| ) |
Post propagator for ![$ z=\diamond_{\mathit{op}}\langle x_0,\dots,x_{n-1}\rangle[y] $](form_415.png) .
.
If y is the empty set, the usual conventions for set operations apply: an empty union is empty, while an empty intersection is the universe, which can be given as the optional parameter u.
The indices for y start at 0.
| void Gecode::element | ( | Home | home, | |
| SetOpType | op, | |||
| const IntVarArgs & | x, | |||
| SetVar | y, | |||
| SetVar | z, | |||
| const IntSet & | u = IntSet(Set::Limits::min, Set::Limits::max) | |||
| ) |
Post propagator for ![$ z=\diamond_{\mathit{op}}\langle \{x_0\},\dots,\{x_{n-1}\}\rangle[y] $](form_416.png) .
.
If y is the empty set, the usual conventions for set operations apply: an empty union is empty, while an empty intersection is the universe, which can be given as the optional parameter u.
The indices for y start at 0.
| void Gecode::element | ( | Home | home, | |
| SetOpType | op, | |||
| const IntSetArgs & | x, | |||
| SetVar | y, | |||
| SetVar | z, | |||
| const IntSet & | u = IntSet(Set::Limits::min, Set::Limits::max) | |||
| ) |
Post propagator for ![$ z=\diamond_{\mathit{op}}\langle x_0,\dots,x_{n-1}\rangle[y] $](form_415.png) .
.
If y is the empty set, the usual conventions for set operations apply: an empty union is empty, while an empty intersection is the universe, which can be given as the optional parameter u.
The indices for y start at 0.
| void Gecode::element | ( | Home | home, | |
| SetOpType | op, | |||
| const IntArgs & | x, | |||
| SetVar | y, | |||
| SetVar | z, | |||
| const IntSet & | u = IntSet(Set::Limits::min, Set::Limits::max) | |||
| ) |
Post propagator for ![$ z=\diamond_{\mathit{op}}\langle \{x_0\},\dots,\{x_{n-1}\}\rangle[y] $](form_416.png) .
.
If y is the empty set, the usual conventions for set operations apply: an empty union is empty, while an empty intersection is the universe, which can be given as the optional parameter u.
The indices for y start at 0.
| void Gecode::element | ( | Home | home, | |
| const SetVarArgs & | x, | |||
| IntVar | y, | |||
| SetVar | z | |||
| ) |
Post propagator for ![$ z=\langle x_0,\dots,x_{n-1}\rangle[y] $](form_417.png) .
.
The indices for y start at 0.
| void Gecode::element | ( | Home | home, | |
| const IntSetArgs & | s, | |||
| IntVar | y, | |||
| SetVar | z | |||
| ) |
Post propagator for ![$ z=\langle s_0,\dots,s_{n-1}\rangle[y] $](form_418.png) .
.
The indices for y start at 0.
| void Gecode::element | ( | Home | home, | |
| const IntSetArgs & | a, | |||
| IntVar | x, | |||
| int | w, | |||
| IntVar | y, | |||
| int | h, | |||
| SetVar | z | |||
| ) |
Post propagator for 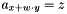 .
.
Throws an exception of type Set::ArgumentSizeMismatch, if 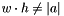 .
.
| void Gecode::element | ( | Home | home, | |
| const SetVarArgs & | a, | |||
| IntVar | x, | |||
| int | w, | |||
| IntVar | y, | |||
| int | h, | |||
| SetVar | z | |||
| ) |
Post propagator for 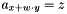 .
.
Throws an exception of type Set::ArgumentSizeMismatch, if 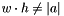 .
.
