Connection constraints to integer variables
[Using finite integer sets]
Functions | |
| void | Gecode::min (Home home, SetVar s, IntVar x) |
| Post propagator that propagates that x is the minimal element of s, and that s is not empty. | |
| void | Gecode::notMin (Home home, SetVar s, IntVar x) |
| Post propagator that propagates that x is not the minimal element of s. | |
| void | Gecode::min (Home home, SetVar s, IntVar x, BoolVar b) |
| Post reified propagator for b iff x is the minimal element of s. | |
| void | Gecode::max (Home home, SetVar s, IntVar x) |
| Post propagator that propagates that x is the maximal element of s, and that s is not empty. | |
| void | Gecode::notMax (Home home, SetVar s, IntVar x) |
| Post propagator that propagates that x is not the maximal element of s. | |
| void | Gecode::max (Home home, SetVar s, IntVar x, BoolVar b) |
| Post reified propagator for b iff x is the maximal element of s. | |
| void | Gecode::channelSorted (Home home, const IntVarArgs &x, SetVar y) |
Post propagator for 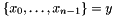 and and 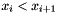 . . | |
| void | Gecode::channel (Home home, const IntVarArgs &x, const SetVarArgs &y) |
Post propagator for 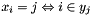 . . | |
| void | Gecode::channel (Home home, const BoolVarArgs &x, SetVar y) |
Post propagator for 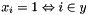 . . | |
| void | Gecode::cardinality (Home home, SetVar s, IntVar x) |
Post propagator for 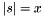 . . | |
| void | Gecode::weights (Home home, IntSharedArray elements, IntSharedArray weights, SetVar x, IntVar y) |
Post propagator for 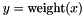 . . | |
Function Documentation
| void Gecode::min | ( | Home | home, | |
| SetVar | s, | |||
| IntVar | x | |||
| ) |
Post propagator that propagates that x is the minimal element of s, and that s is not empty.
| void Gecode::notMin | ( | Home | home, | |
| SetVar | s, | |||
| IntVar | x | |||
| ) |
Post propagator that propagates that x is not the minimal element of s.
| void Gecode::min | ( | Home | home, | |
| SetVar | s, | |||
| IntVar | x, | |||
| BoolVar | b | |||
| ) |
Post reified propagator for b iff x is the minimal element of s.
| void Gecode::max | ( | Home | home, | |
| SetVar | s, | |||
| IntVar | x | |||
| ) |
Post propagator that propagates that x is the maximal element of s, and that s is not empty.
| void Gecode::notMax | ( | Home | home, | |
| SetVar | s, | |||
| IntVar | x | |||
| ) |
Post propagator that propagates that x is not the maximal element of s.
| void Gecode::max | ( | Home | home, | |
| SetVar | s, | |||
| IntVar | x, | |||
| BoolVar | b | |||
| ) |
Post reified propagator for b iff x is the maximal element of s.
| void Gecode::channelSorted | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| SetVar | y | |||
| ) |
Post propagator for 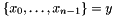 and
and 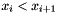 .
.
| void Gecode::channel | ( | Home | home, | |
| const IntVarArgs & | x, | |||
| const SetVarArgs & | y | |||
| ) |
Post propagator for 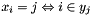 .
.
| void Gecode::channel | ( | Home | home, | |
| const BoolVarArgs & | x, | |||
| SetVar | y | |||
| ) |
Post propagator for 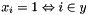 .
.
| void Gecode::cardinality | ( | Home | home, | |
| SetVar | s, | |||
| IntVar | x | |||
| ) |
Post propagator for 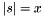 .
.
| void Gecode::weights | ( | Home | home, | |
| IntSharedArray | elements, | |||
| IntSharedArray | weights, | |||
| SetVar | x, | |||
| IntVar | y | |||
| ) |
Post propagator for 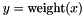 .
.
The weights are given as pairs of elements and their weight: 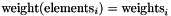
The upper bound of x is constrained to contain only elements from elements. The weight of a set is the sum of the weights of its elements.
