Sorting constraints
[Using finite domain integers]
Collaboration diagram for Sorting constraints:

|
Detailed Description
- Note:
- The Sortedness propagator described in this section only supports bounds-consistency no matter what value for the argument icl is given!
Functions | |
| void | Gecode::sortedness (Space *home, const IntVarArgs &x, const IntVarArgs &y, IntConLevel icl=ICL_DEF) |
Post propagator 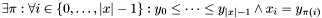 . . | |
| void | Gecode::sortedness (Space *, const IntVarArgs &x, const IntVarArgs &y, const IntVarArgs &z, IntConLevel icl=ICL_DEF) |
Post propagator 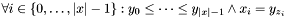 . | |
Function Documentation
|
||||||||||||||||||||
|
Post propagator
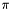 implicit. implicit.
Definition at line 26 of file sortedness.cc. |
|
||||||||||||||||||||||||
|
Post propagator
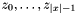 , this interface for Sortedness models the sorting permutation , this interface for Sortedness models the sorting permutation 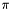 explicitly, such that explicitly, such that 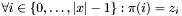 holds. holds.
Definition at line 66 of file sortedness.cc. |
