Cardinality constraints
[Using finite domain integers]
Collaboration diagram for Cardinality constraints:

|
Detailed Description
- Note:
- Domain consistency on the extended cardinality variables of the Global Cardinality Propagator is only obtained if they are bounds consistent, otherwise the problem of enforcing domain consistency on the cardinality variables is NP-complete as proved by Qumiper et. al. in Improved Algorithms for the Global Cardinality Constraint"
Functions | |
| void | Gecode::count (Space *home, const IntVarArgs &x, int n, IntRelType r, int m, IntConLevel icl=ICL_DEF) |
Post propagator for 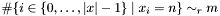 . . | |
| void | Gecode::count (Space *home, const IntVarArgs &x, IntVar y, IntRelType r, int m, IntConLevel icl=ICL_DEF) |
Post propagator for 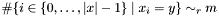 . . | |
| void | Gecode::count (Space *home, const IntVarArgs &x, int n, IntRelType r, IntVar z, IntConLevel icl=ICL_DEF) |
Post propagator for 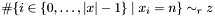 . . | |
| void | Gecode::count (Space *home, const IntVarArgs &x, IntVar y, IntRelType r, IntVar z, IntConLevel icl=ICL_DEF) |
Post propagator for 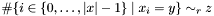 . . | |
| void | Gecode::gcc (Space *home, const IntVarArgs &x, const IntArgs &c, int m, int unspec_low, int unspec_up, int min, int max, IntConLevel icl) |
| Post propagator for
| |
| void | Gecode::gcc (Space *home, const IntVarArgs &x, const IntArgs &c, int m, int unspec, int min, int max, IntConLevel icl) |
| Post propagator for
| |
| void | Gecode::gcc (Space *home, const IntVarArgs &x, int lb, int ub, IntConLevel icl) |
Post propagator for 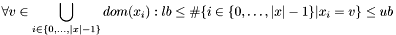 . . | |
| void | Gecode::gcc (Space *home, const IntVarArgs &x, int ub, IntConLevel icl) |
Post propagator for 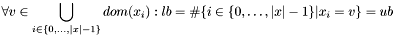 . . | |
| void | Gecode::gcc (Space *home, const IntVarArgs &x, const IntVarArgs &c, int min, int max, IntConLevel icl) |
| Post propagator for
| |
| void | Gecode::gcc (Space *home, const IntVarArgs &x, const IntArgs &v, const IntVarArgs &c, int m, int unspec_low, int unspec_up, bool all, int min, int max, IntConLevel icl) |
Post propagator for 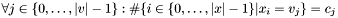 . . | |
| void | Gecode::gcc (Space *home, const IntVarArgs &x, const IntArgs &v, const IntVarArgs &c, int m, int unspec, bool all, int min, int max, IntConLevel icl) |
Post propagator for 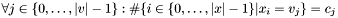 . . | |
Function Documentation
|
||||||||||||||||||||||||||||
|
Post propagator for Supports domain-consistent propagation only. |
|
||||||||||||||||||||||||||||
|
Post propagator for Supports domain-consistent propagation only. |
|
||||||||||||||||||||||||||||
|
Post propagator for Supports domain-consistent propagation only. |
|
||||||||||||||||||||||||||||
|
Post propagator for Supports domain-consistent propagation only. |
|
||||||||||||||||||||||||||||||||||||||||
|
Post propagator for
. Supports value (icl = ICL_VAL, default), bounds (icl = ICL_BND), and domain-consistency (icl = ICL_DOM).
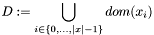 and and 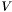 the set of values represented by c. Then this progator allows sets the set of values represented by c. Then this progator allows sets 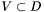 as well as as well as 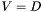 . .
In this interface values
Furthermore, this interface requires that |
|
||||||||||||||||||||||||||||||||||||
|
Post propagator for
. Supports value (icl = ICL_VAL, default), bounds (icl = ICL_BND), and domain-consistency (icl = ICL_DOM).
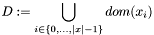 and and 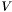 the set of values represented by c. Then this interface allows to specify sets the set of values represented by c. Then this interface allows to specify sets 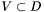 as well as as well as 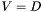 . .
In this interface values |
|
||||||||||||||||||||||||
|
Post propagator for Supports value (icl = ICL_VAL, default), bounds (icl = ICL_BND), and domain-consistency (icl = ICL_DOM).
|
|
||||||||||||||||||||
|
Post propagator for Supports value (icl = ICL_VAL, default), bounds (icl = ICL_BND), and domain-consistency (icl = ICL_DOM).
|
|
||||||||||||||||||||||||||||
|
Post propagator for
.
This interface requires that |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Post propagator for
This interface requires that |
|
||||||||||||||||||||||||||||||||||||||||||||
|
Post propagator for
This interface requires that |

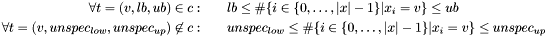
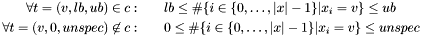
![\begin{eqnarray*} v_j \in I=[min;max] & & \\ \forall j \in \{0, \dots, |I| - 1\}: & & \#\{i\in\{0, \dots, |x| - 1\} | x_i = v_j\} = c_j \end{eqnarray*}](form_227.png)
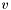 and their cardinality bounds have to specified such that c looks as follows (for example):
and their cardinality bounds have to specified such that c looks as follows (for example): ![$ c=[ (1,0,1), (2,1,3), \dots, (10,4,5)]$](form_221.png) , where the value 1 may occur zero times or once, the value 2 must occur at least once at most three times and the value 10 must occur at least 4 times and at most 5 times.
, where the value 1 may occur zero times or once, the value 2 must occur at least once at most three times and the value 10 must occur at least 4 times and at most 5 times.![$ \forall {i\in\{0, \dots, |x|-1\}}: dom(x_i) \subseteq I=[min;max]$](form_222.png) .
.
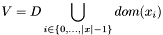
![$ I=[min;max]$](form_229.png)
![$ \forall {i\in\{0, \dots, |x|-1\}}: dom(x_i) \subseteq [min, \dots, max]$](form_230.png) . If all is set to true, every value from the interval
. If all is set to true, every value from the interval