dom.cpp File Reference
#include <gecode/int/dom.hh>#include <gecode/int.hh>#include <gecode/int/rel.hh>Go to the source code of this file.
Namespaces | |
| namespace | Gecode |
Gecode toplevel namespace | |
Functions | |
| void | Gecode::dom (Home home, IntVar x, int n, IntPropLevel ipl=IPL_DEF) |
Propagates 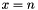 . . | |
| void | Gecode::dom (Home home, const IntVarArgs &x, int n, IntPropLevel ipl=IPL_DEF) |
Propagates 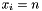 for all for all 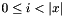 . . | |
| void | Gecode::dom (Home home, IntVar x, int l, int m, IntPropLevel ipl=IPL_DEF) |
Propagates 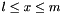 . . | |
| void | Gecode::dom (Home home, const IntVarArgs &x, int l, int m, IntPropLevel ipl=IPL_DEF) |
Propagates 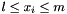 for all for all 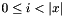 . . | |
| void | Gecode::dom (Home home, IntVar x, const IntSet &s, IntPropLevel ipl=IPL_DEF) |
Propagates 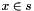 . . | |
| void | Gecode::dom (Home home, const IntVarArgs &x, const IntSet &s, IntPropLevel ipl=IPL_DEF) |
Propagates 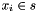 for all for all 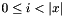 . . | |
| void | Gecode::dom (Home home, IntVar x, int n, Reify r, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for 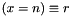 . . | |
| void | Gecode::dom (Home home, IntVar x, int l, int m, Reify r, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for 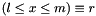 . . | |
| void | Gecode::dom (Home home, IntVar x, const IntSet &s, Reify r, IntPropLevel ipl=IPL_DEF) |
Post domain consistent propagator for 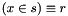 . . | |
| void | Gecode::dom (Home home, IntVar x, IntVar d, IntPropLevel ipl=IPL_DEF) |
| Constrain domain of x according to domain of d. | |
| void | Gecode::dom (Home home, BoolVar x, BoolVar d, IntPropLevel ipl=IPL_DEF) |
| Constrain domain of x according to domain of d. | |
| void | Gecode::dom (Home home, const IntVarArgs &x, const IntVarArgs &d, IntPropLevel ipl=IPL_DEF) |
Constrain domain of 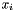 according to domain of according to domain of 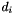 for all for all 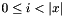 . . | |
| void | Gecode::dom (Home home, const BoolVarArgs &x, const BoolVarArgs &d, IntPropLevel ipl=IPL_DEF) |
Constrain domain of 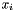 according to domain of according to domain of 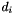 for all for all 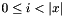 . . | |
